本试题 “动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4,(Ⅰ)求点P的轨迹C的方程;(Ⅱ)过点Q(0,-1)作曲线C的切线,求所作的...” 主要考查您对定积分的简单应用
抛物线的标准方程及图象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 定积分的简单应用
- 抛物线的标准方程及图象
定积分的简单应用:
1、求几何图形的面积:在直角坐标系中,由曲线f(x),直线x=a,x=b(a<b)和x轴围成的曲边梯形的面积,当对应的曲边梯形位于x轴上方时,定积分的取值为正值;当对应的曲边梯形位于x轴下方时,定积分的取值为负值;当位于x轴上方的曲边梯形面积等于位于x轴下方的曲线梯形面积时,定积分的值为0.
2、变速运动问题:如果变速运动的物体的速度v关于时间t的函数是v=v(t)(v(t)≥0),那么物体从时刻t=a到t=b所经过的路程为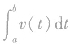 如果变速运动的物体的速度v关于时间t的函数是v=v(t)
如果变速运动的物体的速度v关于时间t的函数是v=v(t)
(v(t)≤0),那么物体从时刻t=a到t=b所经过的路程为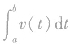 。
。
求定积分的方法:
方法1:用定义求定积分的一般步骤:
(1)分割:n等分区间[a,b];
(2)近似代替:取点ξi∈[xi-1,xi];
(3)求和:
(4)取极限:
方法2:用所求定积分表示的几何意义求积分
当定积分表示的面积容易求时,则利用定积分的几何意义求积分.
抛物线的标准方程及图像(见下表):

抛物线的标准方程的理解:
①抛物线的标准方程是指抛物线在标准状态下的方程,即顶点在原点,焦点在坐标轴上;
②抛物线的标准方程中的系数p叫做焦参数,它的几何意义是:焦点到准线的距离.焦点到顶点以及顶点到准线的距离均为
③抛物线的标准方程有四种类型,所以判断其类型是解题的关键,在方程的类型已确定的前提下,由于标准方程只有一个参数p,所以只需一个条件就可以确定一个抛物线的方程;
④对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,得出其异同点。
共同点:
a.原点在抛物线上;
b.焦点都在坐标轴上;
c.准线与焦点所在轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的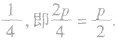
不同点:
a.焦点在x轴上时,方程的右侧为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;
b.开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
求抛物线的标准方程的常用方法:
(1)定义法求抛物线的标准方程:定义法求曲线方程是经常用的一种方法,关键是理解定义的实质及注意条件,将所给条件转化为定义的条件,当然还应注意特殊情况.
(2)待定系数法求抛物线的标准方程:求抛物线标准方程常用的方法是待定系数法,为避免开口不确定,分成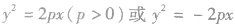 (p>0)两种情况求解的麻烦,可以设成
(p>0)两种情况求解的麻烦,可以设成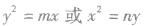 (m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
(m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
与“动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F...”考查相似的试题有:
- 设函数f(x)=ax2+c(a≠0),若∫01f(x)dx=f(x0)0≤x0≤1,则x0的值为( ) A. B.f(x0)a C. D.mm
- 由曲线y=x2和y2=x围成的封闭图形的面积是______.
- 如果用1N的力能将弹簧拉长1cm,为了将弹簧拉长6cm,所耗费的功为[ ]A.0.18JB.0.26JC.0.12JD.0.28J
- 一圆柱形水池盛满了水,将其中上一半的水抽出与下一半的水抽出所需做的功之比为______.
- 若动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则点P的轨迹方程为( )。
- 在△ABC中,B(-2,0),C(2,0),A(x,y)。给出△ABC满足的条件,就能得到动点A的轨迹方程。下表给出了一些条件和方程:条...
- 以双曲线x23-y2=1的右焦点为焦点的抛物线标准方程为______.
- 已知m是非零实数,抛物线C:y2=2px(p>0)的焦点F在直线l:x-my-m22=0上.(I)若m=2,求抛物线C的方程(II)设直线l与抛物...
- 已知椭圆x24+y2b2=1(0<b<2)的离心率等于32,抛物线x2=2py (p>0).(1)若抛物线的焦点F在椭圆的顶点上,求椭圆和抛物...
- 动点M在抛物线2x2=y-1移动,则点A(0,-1)与点M的连线中点的轨迹方程为( ) A.y=3x2 B.y=8x2-1 C.y=4x2 D.y=4x2+1