本试题 “(文科做)已知O为坐标原点,圆心为M的圆的参数方程为点N为圆M上的任意一点,则的取值范围是( ) A.(0,) B.(0,] C.[0,] D.” 主要考查您对用数量积表示两个向量的夹角
参数方程的概念
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
- 参数方程的概念
用数量积表示两个向量的夹角:
设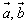 都是非零向量,
都是非零向量,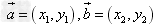 ,θ是
,θ是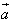 与
与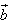 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得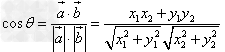 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
参数方程的概念:
一般地,在给定的平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数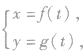 且对于t的每一个允许值,由这个方程组所确定的点M(x,y)都在这条曲线上,那么这个方程组称为这条曲线的参数方程,联系x、y之间关系的变数t称为参变数,简称参数。相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.
且对于t的每一个允许值,由这个方程组所确定的点M(x,y)都在这条曲线上,那么这个方程组称为这条曲线的参数方程,联系x、y之间关系的变数t称为参变数,简称参数。相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.
参数方程和普通方程的互化:
在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致.否则,互化就是不等价的。
(1)参数方程化为普通方程的过程就是消参过程,常见方法有三种:
①代入法:利用解方程的技巧求出参数t,然后代入消去参数;
②三角法:利用三角恒等式消去参数;
③整体消元法:根据参数方程本身的结构特征,从整体上消去.
(2)普通方程化为参数方程需要引入参数.
如:①直线的普通方程是2x-y+2=0,可以化为参数方程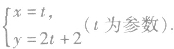
②在普通方程xy=1中,令 可以化为参数方程
可以化为参数方程
关于参数的几点说明:
(1)参数是联系变数x,y的桥梁,可以是一个有物理意义或几何意义的变数,也可以是没有明显实际意义的变数.
(2)同一曲线选取参数不同,曲线参数方程形式也不同.
(3)在实际问题中要确定参数的取值范围.
参数方程的几种常用方法:
方法1参数方程与普通方程的互化:将曲线的参数方程化为普通方程的方法应视题目的特点而定,要选择恰当的方法消参,并要注意由于消参后引起的范围限制消失而造成的增解问题.常用的消参技巧有加减消参,代人消参,平方消参等.
方法2求曲线的参数方程:求曲线的参数方程或应用曲线的参数方程,要熟记曲线参数方程的形式及参数的意义.
方法3参数方程问题的解决方法:解决参数方程的一个基本思路是将其转化为普通方程,然后利用在直角坐标系下解决问题的方式进行解题.
方法4利用圆的渐开线的参数方程求点:利用参数方程求解点时只需将参数代入方程就可求得。
方法5求圆的摆线的参数方程:根据圆的摆线的参数方程的表达式 ,可知只需求出其中的r,也就是说,摆线的参数方程由圆的半径唯一确定,因此只需把点代人参数方程求出r值再代人参数方程的表达式.
,可知只需求出其中的r,也就是说,摆线的参数方程由圆的半径唯一确定,因此只需把点代人参数方程求出r值再代人参数方程的表达式.
与“(文科做)已知O为坐标原点,圆心为M的圆的参数方程为点N为圆...”考查相似的试题有:
- 已知向量a=(cosα,sinα),b=(cosβ,sinβ),且a≠±b,那么a+b与a-b的夹角的大小是______.
- 设非零向量a、b、c满足|a|=|b|=|c|,a+b=c,则<a , b>=______.
- 已知非零向量、满足向量+与向量-的夹角为,那么下列结论中一定成立的是( ) A.= B.||=||, C.⊥ D.∥
- |a|=1,|b|=2,b=c-a,且c⊥a,则a与b的夹角为( )A.60°B.30°C.150°D.120°
- 设向量a与b的夹角为θ,且a=(3,3),2b-a=(-1,1),则cosθ=( )。
- 设向量a,b均为单位向量,且|a+b|=1,则a与b夹角为( )A.π3B.π2C.2π3D.3π4
- 若a=(cosα,sinα),b=(cosβ,sinβ),,且|ka+b|=3|a-kb|(k>0),(1)用k表示数量积a•b;(2)求a•b的最小值,并求出此时a...
- 已知△ABC顶点的直角坐标分别为A(3,4),B(0,0),C(c,0)。(1)若c=5,求sin∠A的值;(2)若∠A是钝角,求c的取值范围。
- 已知曲线C的参数方程是:x=2+2cosθ y=2sinθ (θ为参数),则曲线C的普通方程是______;曲线C被直线x-3y=0所截得的弦长是___...
- 若曲线C1:x=rcosθy=1+rsinθ(θ为参数,r>0)与曲线C2:x=2ty=-2+2t(t为参数)有公共点,则r的取值范围是______.