返回

高中数学

首页
首页 高中数学知识 集合间交、并、补的运算（用Venn图表示） 绝对值不等式 试题正文
  • 单选题
    已知全集U=R，集合A={x|lgx≥0}，B={x||x+1|＞1}，则A∪B=（　　）
    A．（-2，1）B．（-∞，-2）∪（0，+∞）C．[-2，1）D．[1，+∞）

    本题信息：数学单选题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “已知全集U=R，集合A={x|lgx≥0}，B={x||x+1|＞1}，则A∪B=（ ）A．（-2，1）B．（-∞，-2）∪（0，+∞）C．[-2，1）D．[1，+∞）” 主要考查您对

集合间交、并、补的运算（用Venn图表示）

绝对值不等式

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 集合间交、并、补的运算（用Venn图表示）
  • 绝对值不等式

1、交集概念：

（1）一般地，由所有属于集合A且集合B的元素所组成的集合，叫做A与B的交集，记作A∩B，读作A交B，表达式为A∩B＝｛x|x∈A且x∈B｝。
（2)韦恩图表示为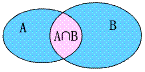
。


2、并集概念：


（1）一般地，由所有属于集合A或集合B的元素所组成的集合，叫做A与B的并集，记作A∪B，读作A并B，表达式为A∪B＝｛x|x∈A或x∈B｝。
（2）韦恩图表示为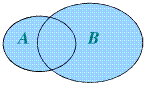
。


3、全集、补集概念：


（1）全集：一般地，如果一个集合含有我们所要研究的各个集合的全部元素，就称这个集合为全集，通常记作U。
        补集：对于一个集合A，由全集U中所有不属于A的元素组成的集合称为集合A相对于全集U的补集，记作CUA，读作U中A的补集，表达式为CUA={x|x∈U，且x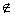A}。
（2）韦恩图表示为
。


1、交集的性质：

 

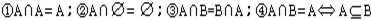
2、并集的性质：

 

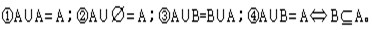
3、补集的性质：

 


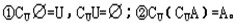
绝对值不等式：

当a>0时，有；
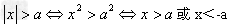或x＜-a 。


绝对值不等式的解法：
 
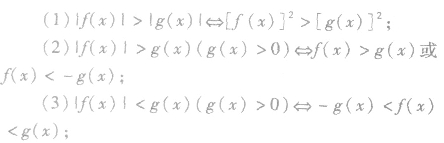
          (4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解，也可以用图象法求解。

发现相似题
与“已知全集U=R，集合A={x|lgx≥0}，B={x||x+1|＞1}，则A∪B=（ ）...”考查相似的试题有：