已知=（-1，x2+m），=（m+1，），当m>0时，求使不等式>0成立的x的取值范围。,高中三年级,数学试题,分式不等式考点,用坐标表示向量的数量积考点,好技网

解答题
已知=（-1，x²+m），=（m+1，），当m>0时，求使不等式>0成立的x的取值范围。

本题信息：2011年0122月考题数学解答题难度较难来源:邵英娜
本题答案
查看答案

本试题 “已知=（-1，x2+m），=（m+1，），当m>0时，求使不等式>0成立的x的取值范围。” 主要考查您对
分式不等式

用坐标表示向量的数量积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

分母恒为正时可去分母；分母不恒为正时不能去分母，应先移项使右边为0再通分并将分子分母分解因式，最后用标根法求解。解分式不等式的主旨是化分式不等式为整式不等式，进行求解。

分式不等式的解法：

分母恒为正时可去分母；分母不恒为正时不能去分母，应先移项使右边为0再通分并将分子分母分解因式，最后用标根法求解。解分式不等式的主旨是化分式不等式为整式不等式，进行求解，即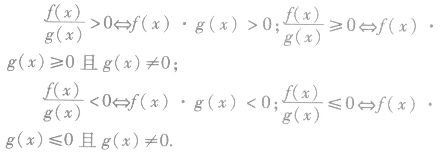

两个向量的数量积的坐标运算:

非零向量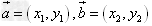，那么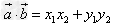，即两个向量的数量积等于它们对应坐标的乘积。

向量的数量积的推广1：

设a=(x,y)，则|a_^|_⁼x²+y²，或|a_^|=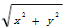

向量的数量积的推广2：

设

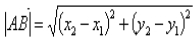
，则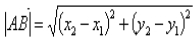

向量的数量积的坐标表示的证明：

已知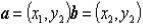

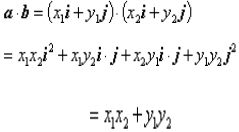
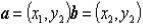，则

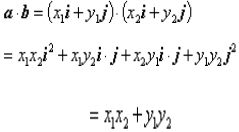
发现相似题

与“已知=（-1，x2+m），=（m+1，），当m>0时，求使不等式>0成立...”考查相似的试题有：