本试题 “将的图象按向量平移,则平移后所得图象的解析式为A.B.C.D.” 主要考查您对函数y=Asin(wx+φ)的图象与性质
向量平移
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数y=Asin(wx+φ)的图象与性质
- 向量平移
函数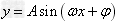 的图象:
的图象:
1、振幅、周期、频率、相位、初相:函数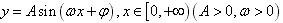 ,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=
,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=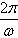 ,称为这个振动的周期,
,称为这个振动的周期,
单位时间内往返振动的次数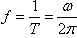 称为振动的频率,
称为振动的频率,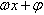 称为相位,x=0时的相位叫初相。
称为相位,x=0时的相位叫初相。
2、用“五点法”作函数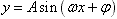 的简图主要通过变量代换,设X=
的简图主要通过变量代换,设X=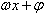 由X取0,
由X取0,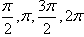 来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
3、函数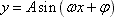 +K的图象与y=sinx的图象的关系:
+K的图象与y=sinx的图象的关系:
把y=sinx的图象纵坐标不变,横坐标向左(φ>0)或向右(φ<0), y=sin(x+φ)
y=sin(x+φ)
把y=sin(x+φ)的图象纵坐标不变,横坐标变为原来的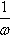 ,
, y=sin(ωx+φ)
y=sin(ωx+φ)
把y=sin(ωx+φ)的图象横坐标不变,纵坐标变为原来的A倍, y=Asin(x+φ)
y=Asin(x+φ)
把y=Asin(x+φ)的图象横坐标不变,纵坐标向上(k>0)或向下(k<0), y=Asin(x+φ)+K;
y=Asin(x+φ)+K;
若由y=sin(ωx)得到y=sin(ωx+φ)的图象,则向左或向右平移 个单位。
个单位。
函数y=Asin(x+φ)的性质:
1、y=Asin(x+φ)的周期为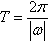 ;
;
2、y=Asin(x+φ)的的对称轴方程是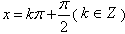 ,对称中心(kπ,0)。
,对称中心(kπ,0)。
点的平移公式:
 ;
;
注:图形F上的任意一点P(x,y)在平移后图形F′上的对应点为P′(x′,y′),且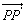 的坐标为(h,k)。
的坐标为(h,k)。
“按向量平移”的几个结论:
(1)点P(x,y)按向量a=(h,k)平移后得到点P′(x+h,y+k);
(2)函数y=f(x)的图象C按向量a=(h,k)平移后得到图象C′,则C′的函数解析式为y=f(x-h)+k;
(3)图象C′按向量a=(h,k)平移后得到图象C,若C的解析式y=f(x),则C′的函数解析式为y=f(x+h)-k;
(4)曲线C:f(x,y)=0按向量a=(h,k)平移后得到图象C′,则C′的方程为f(x-h,y-k)=0;
(5)向量m=(x,y)按向量a=(h,k)平移后得到的向量仍然为m=(x,y)。
与“将的图象按向量平移,则平移后所得图象的解析式为A.B.C.D.”考查相似的试题有:
- 若函数f(x)=3cos(ωx+θ)对任意的x都有f(x)=f(2﹣x),则f(1)等于[ ]A.±3B.0C.3D.﹣3
- 函数y=sin(2x+π3)的图象可由函数y=sin2x的图象经过平移而得到,这一平移过程可以是( )A.向左平移π6B.向右平移π6C.向左...
- 设△ABC的内角A,B,C的对边分别为a,b,c,若bsincos+acos2=a,(1)求角B的大小;(2)设y=sinC-sinA,求y的取值范围.
- 已知函数f(x)=3sin(2x+)+1,(1)求函数f(x)的最小正周期;(2)求函数f(x)的最值及取得最值时的x的取值集合;(3)...
- 函数y=Asin(ωx+φ)在同一区间内的x=π9处取得最大值3,在x=4π9处取得最小值-3,则函数的解析式是( )A.y=3sin(x3-π6)B.y=3...
- 已知函数f(x)=(1+cotx)sin2x﹣2sin(x+)sin(x﹣).(1)若tanα=2,求f(α);(2)若x∈[,],求f(x)的取值范围.
- 已知=(cosx,sinx),=(sinx,cosx),记f(x)=·,要得到函数y=cos2x-sin2x的图象,只需将函数y=f(x)的图象( )A.向左平...
- 将函数y=cos(x-π3)的图象上的各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移π6个单位,所得函数的图象的一条对称轴...
- 设函数f(x)=5sin(k5x-π3)(k≠0).(1)写出f(x)的最大值M,最小值m,最小正周期T;(2)试求最小正整数k,使得当自变量x在任...
- 已知等比数列{an}的公比q=3,前3项和S3=133.(I)求数列{an}的通项公式;(II)若函数f(x)=Asin(2x+φ)(A>0,0<φ<p<...