本试题 “在极坐标系中,点M(4,π3)到曲线ρcos(θ-π3)=2上的点的距离的最小值为 ______” 主要考查您对点到直线的距离
极坐标系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 点到直线的距离
- 极坐标系
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: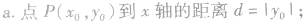
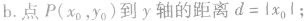
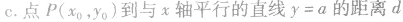

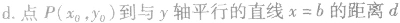
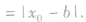
极坐标系的定义:
在平面上取定一点O,称为极点。从O出发引一条射线Ox,称为极轴。再取定一个长度单位,通常规定角度取逆时针方向为正。这样就建立了一个极坐标系。这样,平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定,有序数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ);ρ称为P点的极径,θ称为P点的极角。
点的极坐标:
设M点是平面内任意一点,用ρ表示线段OM的长度,θ表示射线Ox到OM的角度,那么ρ叫做M点的极径,θ叫做M点的极角,有序数对(ρ,θ)叫做M点的极坐标,如图,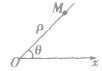
极坐标系的四要素:
极点,极轴,长度单位,角度单位和它的正方向.极坐标系的四要素,缺一不可.
极坐标系的特别注意:
①关于θ和ρ的正负:极角θ的始边是极轴,取逆时针方向为正,顺时针方向为负,θ的值一般以弧度为单位。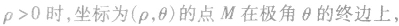


极坐标和直角坐标的互化:
(1)互化的前提条件
①极坐标系中的极点与直角坐标系中的原点重合;
②极轴与x轴的正半轴重合;
③两种坐标系中取相同的长度单位.
(2)互化公式
特别提醒:①直角坐标化为极坐标用第二组公式.通常取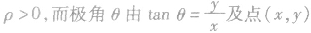 所在的象限取最小正角;
所在的象限取最小正角;
②当
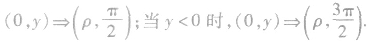
③直角坐标方程及极坐标方程互化时,要切实注意互化前后方程的等价性.
④若极点与坐标原点不是同一个点.如图,设M点在以O为原点的直角坐标系中的坐标为(x,y),在以 为原点也是极点的时候的直角坐标为(x′,y′),极坐标为(ρ,θ),则有
为原点也是极点的时候的直角坐标为(x′,y′),极坐标为(ρ,θ),则有
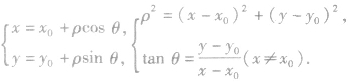
第一组公式用于极坐标化直角坐标;第二组公式用于直角坐标化极坐标.
与“在极坐标系中,点M(4,π3)到曲线ρcos(θ-π3)=2上的点的距离的...”考查相似的试题有:
- 如图所示,已知圆E:x2+(y﹣1)2=4交x轴分别于A,B两点,交y轴的负半轴于点M,过点M作圆E的弦MN.(1)若弦MN所在直线的斜率...
- 在平面直角坐标系xOy中,已知圆:和圆:(1)若直线l过点A(4,0),且被圆C1截得的弦长为2,求直线l的方程;(2)设P为平面上的点,满...
- 已知直线l:ax-y+b=0,圆M:x2+y2-2ax+2by=0,则l与M在同一坐标系中的图形只可能是
- 直线与圆没有公共点,则的取值范围是( )A.B.C.D.
- 已知圆C的方程为,过点M(2,4)作圆C的两条切线,切点分别为A,B,直线AB恰好经过椭圆T:(a>b>0)的右顶点和上顶点.(1...
- 点P(2,3)到直线:ax+(a-1)y+3=0的距离d为最大时,d的值为( )A.7B.5C.3D.1
- 如果圆上总存在两个点到原点的距离为则实数的取值范围是 .
- 当m为参数时,集合A={(x,y)∣x2+y2+x-6y+m=0}是以(-,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交...
- 在直角坐标系中,曲线C的参数方程为(为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,点,直线的极坐标方程为.(1...
- 点M的极坐标是(2,),则M的直角坐标为( ) A.(1,) B.(-,1) C.(,1) D.(-1,)