本试题 “下列命题中,正确的是A.终边相同的角一定相等B.第一象限的角是锐角C.若α-β=2kπ(k∈Z),则角α的三角函数值等于角β的同名三角函数值D.半径为R,α°的圆心角所...” 主要考查您对象限角、轴线角
终边相同的角
弧度制、弧度与角度的互化
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 象限角、轴线角
- 终边相同的角
- 弧度制、弧度与角度的互化
象限角:
在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
轴线角:
如果角的终边在坐标轴上,就认为这个角不属于任何象限,称为轴线角。
第一、二、三、四象限角的集合分别表示为:
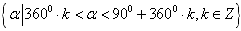 、
、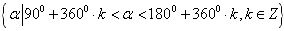 、
、 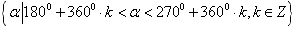 、
、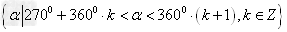 ;
;
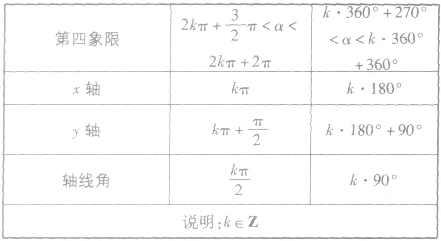
轴线角的集合:
终边在x轴上的角的集合: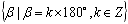 ;
;
终边在y轴上的角的集合: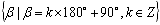 ;
;
终边在坐标轴上的角的集合: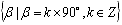 ;
;
已知α是第几象限的角,如何确定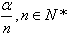 所在象限的角的常用方法:
所在象限的角的常用方法:
(1)分类讨论法,先根据α的范围用整数k把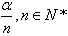 的范围表示出来,再对k分n种情况讨论;
的范围表示出来,再对k分n种情况讨论;
(2)几何法:把各象限均先n等分,再从x轴的正方向的上方起,依次将各区域标上①、②、③、④,则α原来是第几象限对应的标号即为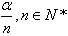 的终边所在的区域。
的终边所在的区域。
常用结论:
(1)已知α所在象限,求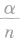
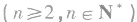 所在象限:通过分类讨论把角写成
所在象限:通过分类讨论把角写成 的形式,然后判断
的形式,然后判断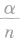 所在象限.
所在象限.
(2)由α所在象限,确定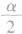 所在象限:
所在象限:
①画出区域:将坐标系每个象限二等分,得8个区域.
②标号:自x轴正向逆时针方向把每个区域依次标上I、Ⅱ、Ⅲ、Ⅳ,如图所示,
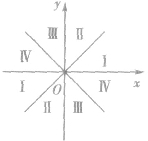
③确定区域:找出与角α所在象限标号一致的区域,即为所求.
(3)由α所在象限,确定 所在象限:
所在象限:
①画出区域:将坐标系每个象限三等分,得到12个区域.
②标号:自x轴正向逆时针方向把每个区域依次标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,如图所示,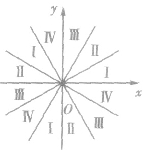
③确定区域:找出与角α所在象限标号一致的区域,即为所求.
终边相同的角的表示:
所有与角α终边相同的角,连同角α在内,可构成一个集合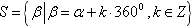 即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
注:(1)k∈Z;
(2)α是任意角;
(3)k?360°与α之间是“+”;
(4)终边相同的角不一定相等,但相等的角的终边一定相同,终边相同的角有无数多个,它们的差是360°的整数倍。
举例说明:
举出画出与30°角的终边相同的一些角吗?390°角的终边、-330°角的终边。
390°=30°+360°
-330°=30°-360°
30°=30°+0×360°
1470°=30°+4×360°
-1770°=30°-5×360°
由特殊角30°看出:所有与30°角终边相同的角,连同30°角自身在内,都可以写成30°+
常见结论:
(1)角α为锐角,则α一定是第一象限的角,反之不一定成立。故角α是锐角是角α为第一象限角的充分不必要条件。
(2)角α为钝角,则α一定是第二象限的角,反之不一定成立。故角α是钝角是角α为第二象限角的充分不必要条件。
(3)第一象限的角不一定是正角。
1弧度的角的概念:
长度等于半径长的弧所对的圆心角叫做1弧度的角,记作1rad。
弧度制:
用弧度作单位来度量角的制度叫弧度制。
一般地:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0。
角α的弧度公式:
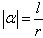 (l表示圆心角α所对的弧长,r表示圆的半径)。
(l表示圆心角α所对的弧长,r表示圆的半径)。
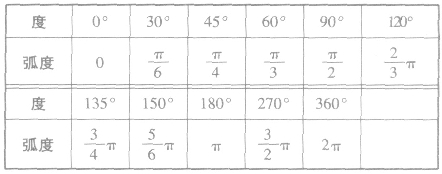
角度与弧度的换算公式:
360°=2π,180°=π,1°=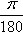 rad≈0.01745rad,1rad=
rad≈0.01745rad,1rad=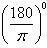 ≈57.30°=57°18′。
≈57.30°=57°18′。
扇形面积公式:
S= lr=
lr= |α|r2。
|α|r2。


与“下列命题中,正确的是A.终边相同的角一定相等B.第一象限的...”考查相似的试题有:
- 下列命题中,命题正确的是A.终边相同的角一定相等B.第一象限的角是锐角C.若α-β=2kπ(k∈Z),则角α的三角函数值等于角β的同...
- 已知△ABC为锐角三角形,则点P(sinA-cosB,cosC-sinB)必位于直角坐标系中的( ) A.第一象限 B.第二象限 C.第三象限 D....
- 已知的周期为2(1)求的最大值以及取最大值时x的集合(2)已知,且,求
- 如图所示,C是半圆弧x2+y2=1(y≥0)上一点, 连接AC并延长至D, 使|CD|=|CB|, 则当C点在半圆弧上从B点移动至A点时,D点所经过的路程...
- 设是第二象限的角,P(x,4)为其终边上的一点,且cosα=,则=( )A.B.C.D.
- 计算= ;
- 已知角a的终边经过点P(3,-4),则sina-2cosa的值是 .
- 角终边上有一点,则下列各点中在角的终边上的点是 ( )A..B..C..D..
- (10分)求值:(1); (2)
- 已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是( )A.B=A∩C B.B∪C=C C.AC D.A=B=C