返回

高中三年级数学

首页
首页 高中三年级数学知识 数列求和的其他方法（倒序相加，错位相减，裂项相加等） 基本不等式及其应用 试题正文
  • 解答题
    已知数列{an}是各项均不为0的等差数列，公差为d，Sn为其前n项和，且满足an2=S2n-1，n∈N﹡．数列{bn}满足，Tn为数列{bn}的前n项和．
    （Ⅰ）求a1，d和Tn；
    （Ⅱ）若对任意的n∈N*，不等式λTnn恒成立，求实数λ的取值范围．
    本题信息：2012年山东省月考题数学解答题难度较难 来源:沈诺（高中数学）
  • 本题答案
    查看答案
本试题 “已知数列{an}是各项均不为0的等差数列，公差为d，Sn为其前n项和，且满足an2=S2n-1，n∈N﹡．数列{bn}满足，Tn为数列{bn}的前n项和．（Ⅰ）求a1，d和Tn；（Ⅱ）若...” 主要考查您对

数列求和的其他方法（倒序相加，错位相减，裂项相加等）

基本不等式及其应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 数列求和的其他方法（倒序相加，错位相减，裂项相加等）
  • 基本不等式及其应用

数列求和的常用方法：

1.裂项相加法：数列中的项形如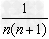的形式，可以把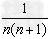表示为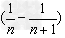，累加时抵消中间的许多项，从而求得数列的和；
2、错位相减法：源于等比数列前n项和公式的推导，对于形如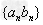的数列，其中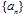为等差数列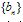，为等比数列，均可用此法；
3、倒序相加法：此方法源于等差数列前n项和公式的推导，目的在于利用与首末两项等距离的两项相加有公因式可提取，以便化简后求和。
4、分组转化法：把数列的每一项分成两项，或把数列的项“集”在一块重新组合，或把整个数列分成两个部分，使其转化为等差或等比数列，这一求和方法称为分组转化法。
5、公式法求和：所给数列的通项是关于n的多项式，此时求和可采用公式求和，常用的公式有：
 
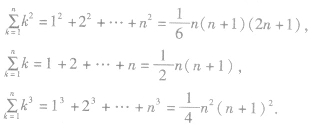
数列求和的方法多种多样，要视具体情形选用合适方法。


数列求和特别提醒：

（1）对通项公式含有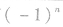的一类数列，在求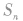时，要注意讨论n的奇偶性；
（2）在用等比数列前n项和公式时，一定要分q=1和q≠1两种情况来讨论。

 

基本不等式：

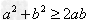（当且仅当a＝b时取“=”号）；
变式：①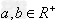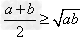，（当且仅当a＝b时取“=”号），即两个正数的算术平均不小于它们的几何平均。
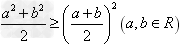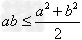②；③；④；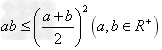


对基本不等式的理解：

(1)基本不等式的证明是利用重要不等式推导的，即，即有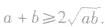
(2)基本不等式又称为均值定理、均值不等式等，其中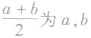的算术平均数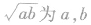，的几何平均数，本定理也可叙述为：两个正数的算术平均数不小于它们的几何平均数．
(3)要特别注意不等式成立的条件和等号成立的条件．均值不等式中：①当a=b时取等号，即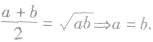


对于两个正数x，y，若已知xy，x+y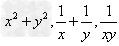，中的某一个为定值，可求出其余各个的最值：
如：（1）当xy＝P（定值），那么当x=y时，和x+y有最小值2，；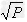
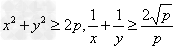（2）x+y=S（定值），那么当x=y时，积xy有最大值，；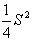
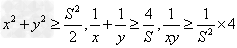（3）已知x2+y2=p，则x+y有最大值为，。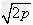

应用基本的不等式解题时：

注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”。

利用基本不等式比较实数大小：

(1)注意均值不等式的前提条件．
(2)通过加减项的方法配凑成使用均值定理的形式．
(3)注意“1”的代换．
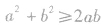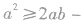
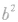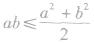(4)灵活变换基本不等式的形式，并注重其变形形式的运用．重要不等式的形式可以是，也可以是，还可以是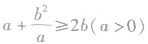等，不仅要掌握原来的形式，还要掌握它的几种变形形式以及公式的逆用等，以便应用．
(5)合理配组，反复应用均值不等式。 


基本不等式的几种变形公式：
 
 

发现相似题
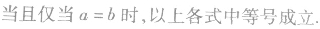
与“已知数列{an}是各项均不为0的等差数列，公差为d，Sn为其前n项...”考查相似的试题有：