本试题 “如图,在△ABC与△ABD中,BC=BD。设点E是BC的中点,点F是BD的中点。(1)请你在图中作出点E和点F;(要求用尺规作图,保留作图痕迹,不写作法与证明)(2)连接...” 主要考查您对三角形全等的判定
垂直平分线的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角形全等的判定
- 垂直平分线的性质
三角形全等判定定理:
1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了
三角形具有稳定性的原因。
2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)
5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边,直角边”) 所以:SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
注意:在全等的判定中,没有AAA和SSA,这两种情况都不能唯一确定三角形的形状。
三角形全等的判定公理及推论:
(1)“边角边”简称“SAS”
(2)“角边角”简称“ASA”
(3)“边边边”简称“SSS”
(4)“角角边”简称“AAS”
注意:在全等的判定中,没有AAA和SSA,这两种情况都不能唯一确定三角形的形状。
要验证全等三角形,不需验证所有边及所有角也对应地相同。
以下判定,是由三个对应的部分组成,即全等三角形可透过以下定义来判定:
①S.S.S. (边、边、边):
各三角形的三条边的长度都对应地相等的话,该两个三角形就是全等。
②S.A.S. (边、角、边):
各三角形的其中两条边的长度都对应地相等,且两条边夹着的角都对应地相等的话,该两个三角形就是全等。
③A.S.A. (角、边、角):
各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等的话,该两个三角形就是全等。
④A.A.S. (角、角、边):
各三角形的其中两个角都对应地相等,且没有被两个角夹着的边都对应地相等的话,该两个三角形就是全等。
⑤R.H.S. / H.L. (直角、斜边、边):
各三角形的直角、斜边及另外一条边都对应地相等的话,该两个三角形就是全等。 但并非运用任何三个相等的部分便能判定三角形是否全等。以下的判定同样是运用两个三角形的三个相等的部分,但不能判定全等三角形:
⑥A.A.A. (角、角、角):
各三角形的任何三个角都对应地相等,但这并不能判定全等三角形,但则可判定相似三角形。
⑦A.S.S. (角、边、边):
各三角形的其中一个角都相等,且其余的两条边(没有夹着该角),但这并不能判定全等三角形,除非是直角三角形。
但若是直角三角形的话,应以R.H.S.来判定。
解题技巧:
一般来说考试中线段和角相等需要证明全等。
因此我们可以来采取逆思维的方式。
来想要证全等,则需要什么条件:要证某某边等于某某边,那么首先要证明含有那两个边的三角形全等。
然后把所得的等式运用(AAS/ASA/SAS/SSS/HL)证明三角形全等。
有时还需要画辅助线帮助解题。常用的辅助线有:倍长中线,截长补短等。
分析完毕以后要注意书写格式,在全等三角形中,如果格式不写好那么就容易出现看漏的现象。
垂直于一条线段并且平分这条线段的直线,叫做这条线段的垂直平分线(中垂线)。
如图:直线MN即为线段AB的垂直平分线。
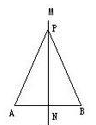
垂直平分线的性质:
1.垂直平分线垂直且平分其所在线段。
2.垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
3.如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。
4.三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相 等。
(此时以外心为圆心,外心到顶点的长度为半径,所作的圆为此三角形的外接圆。)
判定:
①利用定义;
②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(即线段垂直平分线可以看成到线段两端点距离相等的点的集合)
尺规作法:(用圆规作图)
1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。
2、分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线。得到两个交点(两交点交与线段的异侧)。
3、连接这两个交点。
原理:等腰三角形的高垂直平分底边。
与“如图,在△ABC与△ABD中,BC=BD。设点E是BC的中点,点F是BD的中...”考查相似的试题有:
- 如图,已知△ABC中,∠ABC=90 °,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的...
- 如图,已知AC=DB,要使△ABC≌△DCB,则需要补充的条件为_________(填一个即可)
- 如图,E=F=90,B=C,AE=AF,给出下列结论:①1=2; ②BE= CF;③△ACN△ABM;④CD= DN.其中正确的结论是( )(填序号).
- 三角形全等的四种判定方法是:①______②______③______④______.
- 将Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则∠A的度数是( )A. 10°B. 20°C. 25...
- 对于一般三角形全等有( )种判别方法,分别为( )。
- 两组邻边分别相等的四边形我们称它为筝形,如下图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O,(1)求证:①△ABC≌△ADC;②...
- 如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中的全等三角形共有______对.(填数字)
- 如图,二次函数的图象经过点D,与x轴交于A、B两点。(1)求c的值;(2)如图①,设点C为该二次函数的图象在x轴上方的一点,直...
- 如图,在△ABC中,BC边上的垂直平分线交AC于点D;已知AB=3,AC=7,BC=8,则△ABD的周长为______.