反比例函数的图象：
反比例函数的图像是双曲线，它有两个分支，这两个分支分别位于第一、三象限，或第二、四象限，它们关于原点对称。由于反比例函数中自变量x≠0，函数y≠0，所以，它的图像与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。
反比例函数的图像属于以原点为对称中心的中心对称的双曲线，反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交（y≠0）。
反比例函数图象的画法：
（1）列表：

（2）描点：在平面直角坐标系中标出点。
（3）连线：用平滑的曲线连接点。
当双曲线在一三象限，K>0，在每个象限内，Y随X的增大而减小。
当双曲线在二四象限，K<0，在每个象限内，Y随X的增大而增大。
常见画法当两个数相等时那么曲线呈弯月型。
k的意义及应用：
过反比例函数（k≠0），图像上一点P（x,y），作两坐标轴的垂线，两垂足、原点、P点组成一个矩形，矩形的面积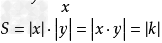。过反比例函数过一点，作垂线，三角形的面积为。
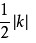研究函数问题要透视函数的本质特征。反比例函数中，比例系数k有一个很重要的几何意义，那就是：过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N则矩形PMON的面积
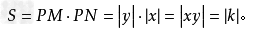
所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数。从而有k的绝对值。在解有关反比例函数的问题时，若能灵活运用反比例函数中k的几何意义，会给解题带来很多方便。

推论内容：一次函数y=x+b或y=-x+b若与反比例函数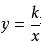存在两个交点，若设2点的横坐标分别为x₁,x₂，那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为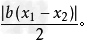
不同象限分比例函数图像：


常见画法：

方差:
是各个数据与平均数之差的平方和的平均数。
在概率论和数理统计中，方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。
在许多实际问题中，研究随机变量和均值之间的偏离程度有着很重要的意义。
设有n个数据各数据x₁，x₂，…，x_n各数据与它们的平均数的差的平方分别是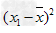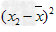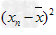，，…，，我们用它的平均数，即用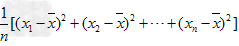来衡量这组数据的波动大小，并把它叫做这组数据的方差，记作。
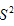方差特点:
（1）设c是常数，则D(c)=0。
（2）设X是随机变量，c是常数，则有D(cX)=(c²)D(X)。
（3）设 X 与 Y 是两个随机变量，则
D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特别的，当X，Y是两个相互独立的随机变量，上式中右边第三项为0（常见协方差），
则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。
（4）D(X)=0的充分必要条件是X以概率为1取常数值c，即P{X=c}=1，其中E(X)=c。
（5）D（aX+bY）=a^2DX+b^2DY+2abE{[X-E(X)][Y-E(Y)]}。

意义：
在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。

标准差：
方差的算术平均根，即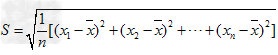，并把它叫做这组数据的标准差，它也是一个用来衡量一组数据的波动大小的重要的量。

公式:
方差是实际值与期望值之差平方的期望值，而标准差是方差算术平方根。 在实际计算中，我们用以下公式计算方差。
方差是各个数据与平均数之差的平方的平均数,即s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]，其中，x_表示样本的平均数，n表示样本的数量，^，xn表示个体，而s^2就表示方差。
而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为样本X的方差的估计时，发现其数学期望并不是X的方差，而是X方差的(n-1)/n倍，[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差，用它作为X的方差的估计具有“无偏性”，所以我们总是用[1/(n-1)]∑(xi-X~)^2来估计X的方差，并且把它叫做“样本方差”。
方差，通俗点讲，就是和中心偏离的程度！用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）并把它叫做这组数据的方差。记作S&sup2.在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。

方差分析主要用途：
①均数差别的显著性检验;
②分离各有关因素并估计其对总变异的作用;
③分析因素间的交互作用;
④方差齐性检验。

一元二次方程的解：
能够使方程左右两边相等的未知数的值叫做方程的解。
解一元二次方程方程：
求一元二次方程解的过程叫做解一元二次方程方程。

韦达定理：
一元二次方程根与系数的关系（以下两个公式很重要，经常在考试中运用到）
一般式：ax2+bx+c=0的两个根x₁和x₂关系：
x₁+x₂= -b/a
x₁·x₂=c/a

一元二次方程的解法：
1、直接开平方法
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如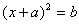的一元二次方程，根据平方根的定义可知，x+a 是b的平方根，当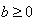时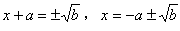，；当b<0时，方程没有实数根。
用直接开平方法求一元二次方程的根，一定要正确运用平方根的性质，即正数的平方根有两个，它们互为相反数，零的平方根是零，负数没有平方根。

2、配方法
配方法是一种重要的数学方法，它不仅在解一元二次方程上有所应用，而且在数学的其他领域也有着广泛的应用。
配方法的理论根据是完全平方公式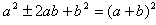，把公式中的a看做未知数x，并用x代替，则有 。

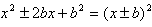3、公式法
公式法是用求根公式解一元二次方程的解的方法，它是解一元二次方程的一般方法。
一元二次方程 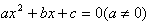的求根公式：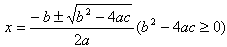
求根公式是专门用来解一元二次方程的，故首先要求a≠0；有因为开平方运算时，被开方数必须是非负数，所以第二个条件是b²-4ac≥0。即求根公式使用的前提条件是a≠0且b²-4ac≥0。

4、因式分解法
因式分解法就是利用因式分解的手段，求出方程的解的方法，这种方法简单易行，是解一元二次方程最常用的方法。