本试题 “已知函数f(x)=(xa-1)2+(bx-1)2,x∈D,其中0<a<b.(1)当D=(0,+∞)时,设t=xa+bx,f(x)=g(t),求y=g(t)的解析式及定义域;(2)当D=(0,+∞),a=1...” 主要考查您对函数的奇偶性、周期性
二次函数的性质及应用
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的奇偶性、周期性
- 二次函数的性质及应用
- 基本不等式及其应用
函数的奇偶性定义:
偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性:
(1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。
奇函数与偶函数性质:
(1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。
注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
2、函数的周期性 令a , b 均不为零,若:
(1)函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
(2)函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
(3)函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
(4)函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|2a|
==> 函数最小正周期 T=|2a|
(5)函数y = f(x) 存在 f(x + a) = 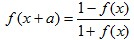 ==> 函数最小正周期 T=|4a|
==> 函数最小正周期 T=|4a|
二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于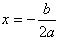 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴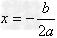 ;
;
③有顶点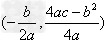 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
①当a>0时,函数f(x)的图象开口向上,在(-∞,-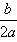 )上是减函数,在[-
)上是减函数,在[- ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-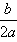 )上是增函数,在[-
)上是增函数,在[-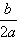 ,+∞)是减函数。
,+∞)是减函数。
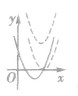
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
 |
值域 | a>0 | a<0 |
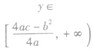 |
 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
| a<0 | 单调性 | a>0 | a<0 |
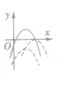 |
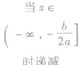 |
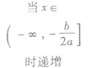 | |
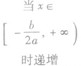 |
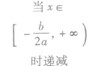 | ||
| 图像特点 |
 | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为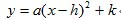 ;
;
(3)双根式:若相应一元二次方程的两个根为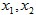 ,则其解析式为
,则其解析式为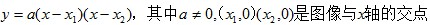 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
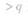 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令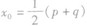 .
.
①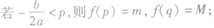
②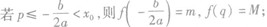
③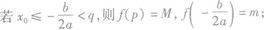
④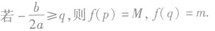
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数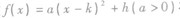 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
基本不等式:
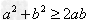 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①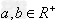 ,
,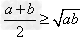 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②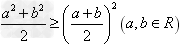 ;③
;③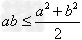 ;④
;④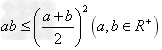 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有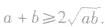
(2)基本不等式又称为均值定理、均值不等式等,其中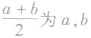 的算术平均数,
的算术平均数,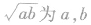 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即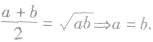
对于两个正数x,y,若已知xy,x+y,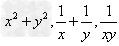 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2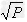 ,
,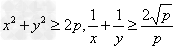 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值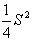 ,
,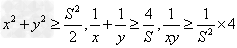 ;
;
(3)已知x2+y2=p,则x+y有最大值为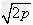 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式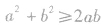 的形式可以是
的形式可以是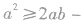
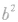 ,也可以是
,也可以是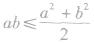 ,还可以是
,还可以是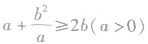 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

与“已知函数f(x)=(xa-1)2+(bx-1)2,x∈D,其中0<a<b.(1)当D=...”考查相似的试题有:
- 若,定义:,例如,则函数A.是偶函数B.是奇函数C.既是奇函数也是偶函数D.既不是奇函数也不是偶函数
- 已知命题P:∃x∈R,x2+2ax+a≤0.若命题p是假命题,则实数a的取值范围是( ) A.(-∞,0]∪[1,+∞) B.[0,1] C.(-∞,0)∪(...
- 已知f(x)是定义在[-1,1]上的偶函数,且在(0,1]上单调递增,则不等式f(1-x)<f(x2-1)的解集是______.
- 定义在R上的函数y=f(x),满足f(3-x)=f(x),(x-)f′(x)<0,若x1<x2,且x1+x2>3,则有[ ]A.f(x1)<f(x2)B.f(x1)>f(x2)C.f...
- 已知x∈[2,3],则函数f(x)=4x-2x+1的值域为______.
- 对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为:)为0.8,要求洗完后的清洁度是0.99.有两种方案可供...
- 已知,且函数在处有极值,则的最大值等于( )A.B.3C.6D.9
- 已知函数f(x)=x3+2ax2+1ax,(a>0),则f(2)的最小值为( )A.1232B.16C.8+8a+2aD.12+8a+1a
- 已知椭圆的左右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P,(Ⅰ)设P点...
- 已知x、y都是正数,则满足x+2y+xy=30,求xy的最大值,并求出此时x、y的值.