本试题 “已知三棱锥O-ABC,∠BOC=90°,OA⊥平面BOC,其中OA=1,OB=2,OC=3,O,A,B,C四点均在球S的表面上,则球S的表面积为( )。” 主要考查您对球的表面积与体积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 球的表面积与体积
球的体积公式:
V球=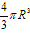 ;
;
球的表面积:
S球面=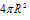
求球的表面积和体积的关键:
由球的表面积和体积公式可知,求球的表面积和体积的关键是求出半径。
常用结论:
1.若球的表面积变为原来的2倍,则半径变为原来的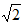 倍.
倍.
2.若球半径变为原来的2倍,则表面积变为原来的4倍.
3.若两球表面积之比为1:2,则其体积之比是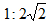 .
.
4.若两球体积之比是1:2,则其表面积之比是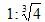 .
.
发现相似题
与“已知三棱锥O-ABC,∠BOC=90°,OA⊥平面BOC,其中OA=1,OB=2,OC...”考查相似的试题有:
- 正四棱锥S-ABCD的底面边长和各侧棱长都为2,点S、A、B、C、D都在同一个球面上,则该球的体积为______.
- 如图所示,正四棱锥P-ABCD的底面积为3,体积为,E为侧棱PC的中点,则PA与BE所成的角为__________.
- 设地球半径为R,在北纬60°圈上有A、B两地,它们在纬度圈上的弧长是,则这两地的球面距离是( ). A.B.C.D.
- 正方体的内切球的体积为, 则此正方体的表面积是A.216B.72C.108D.648
- 如图是一个正三棱柱体的三视图,该柱体的体积等于A.B.2C.2D.
- 一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,则这...
- 已知球的表面积为12π,则该球的体积是______.
- 将一个钢球置于由6根长度为2m(应该是6)的钢管焊接成的正四面体的钢架内,那么,这个钢球的最大体积为______(m3).
- 圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示...
- 若与球心距离为4的平面截球所得的截面圆的面积是9π,则球的表面积是______