本试题 “下列命题中①若|a•b|=|a|•|b|,则a∥b;②a=(-1,1)在b=(3,4)方向上的投影为15;③若△ABC中,a=5,b=8,c=7则BC•CA=20;④若非零向量a、b满足|a+b|=b,则|2b|...” 主要考查您对向量共线的充要条件及坐标表示
向量数量积的含义及几何意义
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量共线的充要条件及坐标表示
- 向量数量积的含义及几何意义
- 向量数量积的运算
向量共线的充要条件:
向量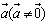 与
与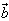 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得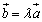 。
。
向量共线的几何表示:
设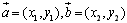 ,其中
,其中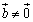 ,当且仅当
,当且仅当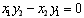 时,向量
时,向量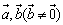 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
两个向量的夹角的定义:
对于非零向量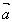 ,
,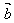 ,作
,作 称为向量
称为向量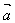 ,
,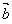 的夹角,当
的夹角,当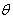 =0时,
=0时,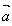 ,
,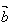 同向,当
同向,当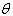 =π时,
=π时,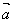 ,
,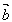 反向,
反向,
当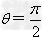 时,
时,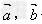 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积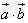 等于
等于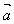 的模
的模 与
与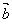 在
在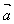 上的投影
上的投影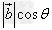 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量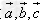 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)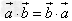 ;
;
(2)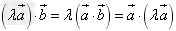 ;
;
(3)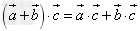 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
与“下列命题中①若|a•b|=|a|•|b|,则a∥b;②a=(-1,1)在b=(3,4...”考查相似的试题有:
- 已知椭圆C的方程为,椭圆C的左、右焦点分别为F1(-1,0)、F2(1,0),斜率为k(k≠0)的直线l经过点F2,交椭圆于A、B两点,...
- 已知向量的夹角为,,,则 。
- 已知向量满足,且,,则a与b的夹角为 .
- (本题12分),其中.(1)求的取值范围;(2)若函数的大小
- 已知空间向量,,则_________.
- 已知,若,则k= .
- 已知正方形的边长为,记以为起点,其余顶点为终点的向量分别为,,.若且,则的所有可能取值为 .
- 若a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是( )A.B.C.D.
- 已知直线ax+by+c=0与圆O:x2+y2=1相交于A、B两点,且|AB|=,则=( )。
- 已知圆O的半径为1,PA,PB为该圆的两条切线,A,B为切点,那么的最小值是 A.-4+B.-3+C.-4+2D.-3+2