本试题 “如图为双曲线的两焦点,以为直径的圆与双曲线交于是圆与轴的交点,连接与交于,且是的中点,(1)当时,求双曲线的方程; (2)试证:对任意的正实数,双曲线...” 主要考查您对双曲线的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 双曲线的定义
双曲线第一定义:
平面内与两定点F1,F2的距离的差的绝对值等于定长2a(小于|F1F2|)的点的轨迹叫双曲线,即||PF1|-|PF2||=2a(2a<|F1F2|)。若2a=|F1F2|,则轨迹是以F1,F2为端点射线,若2a>|F1F2|,则轨迹不存在;若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
双曲线的第二定义:
平面内与一个定点F和一条定直线l的距离的比是常数e(e>1)的动点的轨迹叫双曲线。
双曲线的理解:
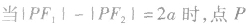 的轨迹为近
的轨迹为近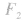 的一支;
的一支;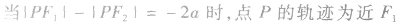 的一支。
的一支。
注: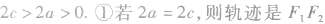 的延长线和反向延长线(两条射线);
的延长线和反向延长线(两条射线);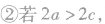 则轨迹不存在;
则轨迹不存在; 的垂直平分线。
的垂直平分线。
发现相似题
与“如图为双曲线的两焦点,以为直径的圆与双曲线交于是圆与轴的...”考查相似的试题有:
- 已知是双曲线的左、右焦点,为双曲线左支上一点,若的最小值为,则该双曲线的离心率的取值范围是A.B.C.D.
- 等轴双曲线的中心在原点,焦点在轴上,与抛物线的准线交于两点,;则的实轴长为( )A.B.C.D.
- A.圆B.椭圆C.双曲线一支D.抛物线
- 双曲线x216-y29=1上的点P到点(5,0)的距离是6,则点P的坐标是( )A.(8,±33)B.(8,-3)C.(8,3)D.(8,±3)
- 若双曲线的离心率为2,则的值为 .
- 中心在原点的双曲线,一个焦点为,一个焦点到最近顶点的距离是,则双曲线的方程是( )A.B.C.D.
- 已知双曲线中心在原点,右焦点与抛物线的焦点重合,则该双曲线的离心率为___________
- 以知F是双曲线的左焦点,是双曲线右支上的动点,则的最小值为
- .双曲线的渐近线与圆相切,则( )A.2B.C.D.4
- 双曲线x29-y25=1的焦距为______