本试题 “若对任意的x∈A,y∈B,(AR,BR),有唯一确定的f(x,y)与之对应,则称f(x,y)为关于x、y的二元函数。现定义满足下列性质的二元函数f(x,y)为关于实数x、y的广义...” 主要考查您对函数的定义域、值域
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则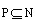 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如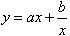 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
发现相似题
与“若对任意的x∈A,y∈B,(AR,BR),有唯一确定的f(x,y)与之对应...”考查相似的试题有:
- 函数的最小值为,求的解析式.
- 已知函数f(x)=lg(3+x)+lg(3-x).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性.
- 下列函数中值域是(0,+∞)的函数是 ( )A.B.C.D.
- 设x∈(0,π),则函数y=sinx2+2sinx的最小值是( )A.2B.94C.52D.3
- 函数y=x2-2x-3,x∈(-1,2]的值域为______.
- 已知函数f(2x)的定义域[1、2],则f(log2x)的定义城是.( )A.[0、1]B.[1、2]C.[2、4]D.[4、16]
- 函数f(x)=2x-x2(2x-1)+(3-2x)0的定义域为______:
- 已知函数f(x)=1-22x+t(t是常实数).(1)若函数的定义为R,求y=f(x)的值域;(2)若存在实数t使得y=f(x)是奇函数,证明...
- 函数的定义域为A.B.C.D.
- (本题满分10分)求下列函数的定义域