本试题 “在△ABC中,角A,B,C所对的边分别为a,b,c,向量m=(a,b),n=(cosA,cosB),p=(,2sinA),若m∥n,|p|2=9,试判断△ABC的形状。” 主要考查您对正弦定理
向量共线的充要条件及坐标表示
向量模的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
- 向量共线的充要条件及坐标表示
- 向量模的计算
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即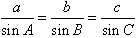 =2R。
=2R。
有以下一些变式:
(1)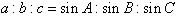 ;
;
(2)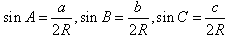 ;
;
(3)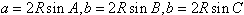 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 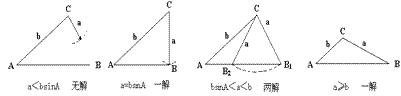
也可根据a,b的关系及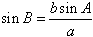 与1的大小关系来确定。
与1的大小关系来确定。
向量共线的充要条件:
向量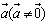 与
与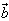 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得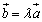 。
。
向量共线的几何表示:
设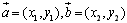 ,其中
,其中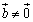 ,当且仅当
,当且仅当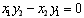 时,向量
时,向量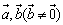 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
向量的模:
设 ,则有向线段
,则有向线段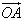 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: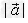 ,则
,则  。
。
向量模的坐标表示:
(1)若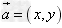 ,则
,则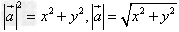 ;
;
(2)若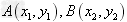 ,那么
,那么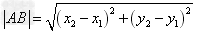 。
。
求向量的模:
求向量的模主要是利用公式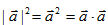 来解。
来解。
发现相似题
与“在△ABC中,角A,B,C所对的边分别为a,b,c,向量m=(a,b)...”考查相似的试题有:
- 在△ABC中,角A,B,C所对的边分别为a,b,c,若角A,B,C依次成等差数列,a=1,b=,则S△ABC等于 ( ).A.B.C.D.2
- 在△ABC中,a,b,c分别是角A,B,C所对的边,且3a=2csinA,则角C的大小为______.
- 已知a,b,c分别为△ABC的三个内角A,B,C的对边,=(sinA,1),=(cosA,),且∥.(1)求角A的大小;(2)若a=2,b=2,...
- 若的内角满足,则的最小值是 .
- 黑板上有一道有正解的解三角形的习题,一位同学不小心把其中一部分擦去了,现在只能看到:在△ABC中,角A,B,C的对边分别为a...
- 中,,,则( )A.B.C.D.
- 在△ABC中,A=60°,b=16,面积S=2203,则a等于( )A.106B.75C.49D.51
- 如图,四点A、B、C、D共圆,AC与BD相交于M,BC=,AD=1+,∠ADB=60°,∠CBD=15°,则AB的长为[ ]A、B、C、+D、2+
- 设平面向量=(1,2),=(-2,y),若∥,则|3+|等于( ) A. B. C. D.
- 在平行四边形ABCD中,若|+|=|-|,则必有( ) A.= B.=或= C.ABCD是矩形 D.ABCD是正方形