本试题 “设函数f(x)=2sin(ωx+π4)(ω>0)与函数g(x)=cos(2x+ϕ)(|ϕ|≤π2)的对称轴完全相同,则ϕ的值为( )A.π4B.-π4C.π2D.-π2” 主要考查您对正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
正弦函数和余弦函数的图象:正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的图象分别叫做正弦曲线和余弦曲线,
1.正弦函数 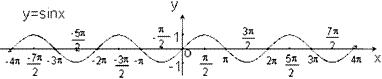
2.余弦函数
函数图像的性质
正弦、余弦函数图象的性质: 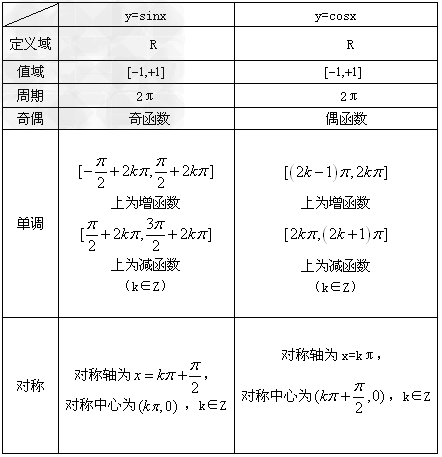
由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当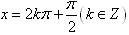 时,y取最大值1,
时,y取最大值1,
当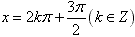 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
正弦、余弦函数图象的性质:

由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当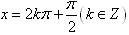 时,y取最大值1,
时,y取最大值1,
当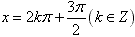 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
发现相似题
与“设函数f(x)=2sin(ωx+π4)(ω>0)与函数g(x)=cos(2x+ϕ)(|ϕ|≤π2)...”考查相似的试题有:
- 的图象的一段如图所示,它的解析式是( )A.B.C.D.
- 函数的单增区间是___________.
- 函数单调增区间为( )A.B.C.D.
- 函数()的最小正周期为_____,最大值为____.
- (12分)已知函数f(X)=sin2X+acos2X (aR) 且是函数Y=f(X)的零点(1)求a的值,并求函数f(X)的最小正周期(2)若X〔0,〕,...
- 既是偶函数又在区间上单调递减的函数是( )A.B.C.D.
- 已知函数f(x)=cos(2x+ϕ)满足f(x)≤f(1)对x∈R恒成立,则( )A.函数f(x+1)一定是偶函数B.函数f(x-1)一定是偶函数...
- 已知tan,tan是方程的两根,则tan(+)=___
- (本小题满分12分)函数的一系列对应值如下表:。。。0。。。。。。010—10。。。(1)根据表中数据求出的解析式;(2)指出函...
- 若函数f(x)=sin2(x+π4)+cos2(x-π4)-1,则函数f(x)是( )函数.A.周期为π的偶B.周期为2π的偶C.周期为2π的奇D.周期为π的奇