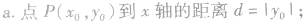
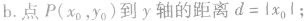
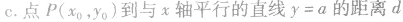
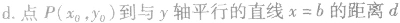
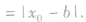
参数方程的概念：
一般地，在给定的平面直角坐标系中，如果曲线上任意一点的坐标x，y都是某个变数t的函数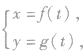 且对于t的每一个允许值，由这个方程组所确定的点M（x，y）都在这条曲线上，那么这个方程组称为这条曲线的参数方程，联系x、y之间关系的变数t称为参变数，简称参数。相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程．

参数方程和普通方程的互化：

在参数方程与普通方程的互化中，必须使x，y的取值范围保持一致．否则，互化就是不等价的。
（1）参数方程化为普通方程的过程就是消参过程，常见方法有三种：
①代入法：利用解方程的技巧求出参数t，然后代入消去参数；
②三角法：利用三角恒等式消去参数；
③整体消元法：根据参数方程本身的结构特征，从整体上消去．
(2)普通方程化为参数方程需要引入参数．
如：①直线的普通方程是2x-y+2=0，可以化为参数方程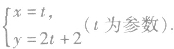 
②在普通方程xy=1中，令可以化为参数方程

关于参数的几点说明：

(1)参数是联系变数x，y的桥梁，可以是一个有物理意义或几何意义的变数，也可以是没有明显实际意义的变数．
(2)同一曲线选取参数不同，曲线参数方程形式也不同．
(3)在实际问题中要确定参数的取值范围．

参数方程的几种常用方法：

方法1参数方程与普通方程的互化：将曲线的参数方程化为普通方程的方法应视题目的特点而定，要选择恰当的方法消参，并要注意由于消参后引起的范围限制消失而造成的增解问题．常用的消参技巧有加减消参，代人消参，平方消参等．
方法2求曲线的参数方程：求曲线的参数方程或应用曲线的参数方程，要熟记曲线参数方程的形式及参数的意义．
方法3参数方程问题的解决方法：解决参数方程的一个基本思路是将其转化为普通方程，然后利用在直角坐标系下解决问题的方式进行解题．
方法4利用圆的渐开线的参数方程求点：利用参数方程求解点时只需将参数代入方程就可求得。
方法5求圆的摆线的参数方程：根据圆的摆线的参数方程的表达式，可知只需求出其中的r，也就是说，摆线的参数方程由圆的半径唯一确定，因此只需把点代人参数方程求出r值再代人参数方程的表达式．

圆的参数方程：

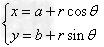（θ∈[0，2π）），（a，b）为圆心坐标，r为圆的半径，θ为参数（x，y）为经过点的坐标。

 

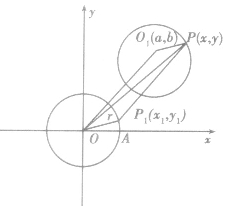
圆心为原点，半径为r的圆的参数方程：

如图，如果点P的坐标为(x，y)，圆半径为r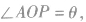， 根据三角函数定义，点P的横坐标x、纵坐标y都是θ的函数，即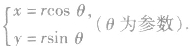
 

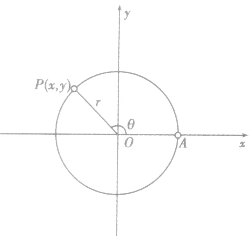
直线的参数方程：

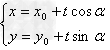过定点倾斜角为α的直线的参数方程为（t为参数）。

直线的参数方程及其推导过程：

设e是与直线l平行且方向向上(l的倾斜角不为0)或向右（l的倾斜角为0）的单位方向向量（单位长度与坐标轴的单位长度相同）．直线l的倾斜角为α，定点M₀、动点M的坐标分别为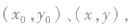
 

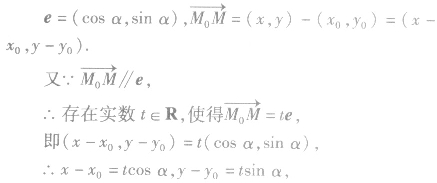
直线的参数方程中参数t的几何意义是：表示参数t对应的点M到定点Mo的距离，当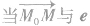同向时，t取正数；当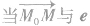异向时，t取负数；当点M与Mo重合时，t=0．