本试题 “如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:(1)PC∥平面EBD.(2)平面PBC⊥平面PCD.” 主要考查您对直线与平面平行的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线与平面平行的判定与性质
线面平行的定义:
若直线和平面无公共点,则称直线和平面平行。
图形表示如下:
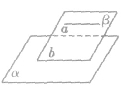
线面平行的判定定理:
平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。 线线平行 线面平行
线面平行
符号语言:
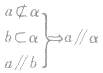
线面平行的性质定理:
如果一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。 线面平行 线线平行
线线平行
符号语言:
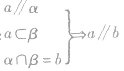
证明直线与平面平行的常用方法:
(l)反证法,即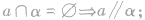
(2)判定定理法,即
(3)面面平行的性质定理,即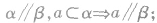
(4)向量法,平面外的直线 的方向向量n与平面
的方向向量n与平面 的法向量n垂直,则直线
的法向量n垂直,则直线 与平面
与平面 平行,即
平行,即
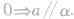
发现相似题
与“如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是P...”考查相似的试题有:
- 已知在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.(1)求证:AF∥平面PEC;(2...
- 如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O。将菱形ABCD沿对角线AC折起,使BD=3,得到三棱锥B-ACD,(Ⅰ)若点M是棱BC的...
- 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.(Ⅰ)求证:AE⊥平面BCE;(Ⅱ)求证;AE∥平面BFD;(...
- 空间四边形ABCD中,E,F,G,H分别AB,BC,CD,AD的中点,求证:EH∥平面BCD.
- 已知a ,b ,l,表示三条不同的直线,α,β,γ表示三个不同平面,给出下列四个命题:①若α∩β=a ,γ∩ β=b ,且a ∥b ,则α∥γ;②若...
- 若l为一条直线,α,β,γ为三个互不重合的平面,给出下面三个命题:①α⊥γ,β⊥γα⊥β;②α⊥γ,β∥γα⊥β;③l∥α,l⊥βα⊥β;其中正确的命...
- 已知如图几何体,矩形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE。(Ⅰ)求证:CF∥平面MBD;(Ⅱ)求证...
- 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.(1)在直线BC上是否存在一点P,使得D...
- 如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.(I)设E是DC的中点,求证:D1E∥平面A1BD;(II)求...
- 如图所示,多面体EF-ABCD中,ABCD是梯形,AB∥CD,ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=AE=a,∠ACB=。(1)求证:BC⊥平面...