本试题 “在等比数列{an}中,a4a1=,则tan(a2a3)=( ) A.- B.- C. D.” 主要考查您对正切、余切函数的图象与性质(定义域、值域、单调性、奇偶性等)
等比数列的通项公式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正切、余切函数的图象与性质(定义域、值域、单调性、奇偶性等)
- 等比数列的通项公式
正切函数的图像:
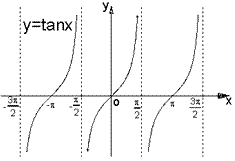
余切函数的图像:
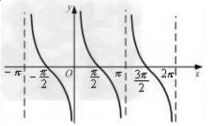
正切函数的性质:
(1)定义域: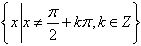 ;
;
(2)值域是R,在上面定义域上无最大值也无最小值;
(3)周期性:是周期函数且周期是π,它与直线y=a的两个相邻交点之间的距离是一个周期π;
(4)奇偶性:是奇函数,对称中心是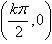 (k∈Z),无对称轴;
(k∈Z),无对称轴;
(5)单调性:正切函数在开区间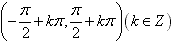 内都是增函数。但要注意在整个定义域上不具有单调性。
内都是增函数。但要注意在整个定义域上不具有单调性。
余切函数的性质:
(1)定义域:{x|x≠kπ,k∈Z}
(2)值域:实数集R;
(3)周期性:是周期函数,周期为kπ(k∈Z且k≠0),最小正周期T=π
(4)奇偶性:奇函数,图像关于( ,0)(k∈z)对称,实际上所有的零点都是它的对称中心
,0)(k∈z)对称,实际上所有的零点都是它的对称中心
(5)单调性:在每一个开区间(kπ,(k+1)π),(k∈Z)上都是减函数,在整个定义域上不具有单调性
等比数列的通项公式:
an=a1qn-1,q≠0,n∈N*。
等比数列的通项公式的理解:
①在已知a1和q的前提下,利用通项公式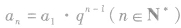 可求出等比数列中的任意一项;
可求出等比数列中的任意一项;
②在已知等比数列中任意两项的前提下,使用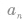
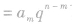 可求等比数列中任何一项;
可求等比数列中任何一项;
③用函数的观点看等比数列的通项,等比数列{an}的通项公式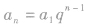 ,可以改写为
,可以改写为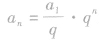 .当q>o,且q≠1时,y=qx是一个指数函数,而
.当q>o,且q≠1时,y=qx是一个指数函数,而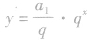 是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数
是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数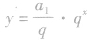 的图象上的一群孤立的点;
的图象上的一群孤立的点;
④通项公式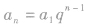 亦可用以下方法推导出来:
亦可用以下方法推导出来: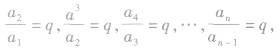
将以上(n一1)个等式相乘,便可得到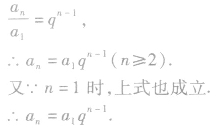
⑤用方程的观点看通项公式.在an,q,a1,n中,知三求一。
发现相似题
与“在等比数列{an}中,a4a1=,则tan(a2a3)=( ) A.- B.- C...”考查相似的试题有:
- 在中,角所对的边分别为,且(1)求函数的最大值;(2)若,求的值.
- 要得到函数的图象,只需将函数的图象( )A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位
- (13分)△ABC中,分别是角A,B,C的对边,且.(1)求; (2)若,且,求△ABC的面积.
- (本小题满分12分)已知,其中,.(1)求的最小正周期;(2)求图象的对称中心;(3)求在上的单调递减区间.
- 已知函数 ,则、、的大小关系A >> B >>C >> D >>
- 已知函数,给出下列四个命题:①函数是周期函数,②函数既有最大值又有最小值,③函数的图像有对称轴,④对于任意,函数的导函数。...
- (本题满分12分)已知函数的部分图象如图所示.(Ⅰ) 求函数的解析式;(Ⅱ) 如何由函数的图象通过适当的变换得到函数的图象, 写出...
- 等比数列{an}满足:a1+a6=11,a3•a4=239,且公比q∈(0,1),则数列的{an}通项公式为______.
- 在等比数列{an}中,a1=2,a4=16(1)求数列{an}的通项公式;(2)令bn=1log 2an •log2an+1,n∈N*,求数列{bn}的前n项和Sn.
- 已知等差数列{an}的前n项和为An,且满足a1+a5=6,A9=63;数列{bn}的前n项和为Bn,且满足Bn=2bn-1(n∈N*).(I)求数列{an},{b...