本试题 “如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为a,(1)建立适当的坐标系,并写出点A、B、A1、C1的坐标;(2)求AC1与侧面ABB1A1所成的角。” 主要考查您对在空间直角坐标系表示点的位置
用向量方法解决线线、线面、面面的夹角问题
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 在空间直角坐标系表示点的位置
- 用向量方法解决线线、线面、面面的夹角问题
单位正交基底:
若空间一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,通常用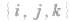 表示.
表示.
空间中点的坐标的定义:
如图,OBCD-D′A′B′C′是单位正方体,以A为原点,分别以OD,OA′,OB的方向为正方向,建立三条数轴x轴,y轴,z轴,这时建立了一个空间直角坐标系O-xyz, 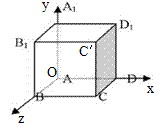
1)O叫做坐标原点;
2)x 轴,y轴,z轴叫做坐标轴;
3)过每两个坐标轴的平面叫做坐标平面;
2、右手表示法:令右手大拇指、食指和中指相互垂直时,可能形成的位置。大拇指指向为x轴正方向,食指指向为y轴正向,中指指向则为z轴正向,这样也可以决定三轴间的相位置。
3、任意点坐标表示:空间一点M的坐标可以用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标,记作M(x,y,z)(x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标)。
空间直角坐标系的建立:
在空间中选定一点O和一个单位正交基底 (如图所示).以点O为原点,分别以
(如图所示).以点O为原点,分别以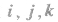 的方向为正方向建立三条数轴:x轴,y轴,z轴,它们都叫做坐标轴,这时我们说建立了一个空间直角坐标系O-xyz,点O叫做原点,向量
的方向为正方向建立三条数轴:x轴,y轴,z轴,它们都叫做坐标轴,这时我们说建立了一个空间直角坐标系O-xyz,点O叫做原点,向量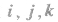 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为xOy平面,yOz平面,zOx平面.
都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为xOy平面,yOz平面,zOx平面.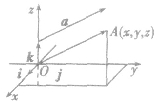
空间直角坐标系的画法:
作空间直角坐标系O-xyz,一般使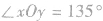 (或450),
(或450),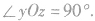
异面直线所成角:
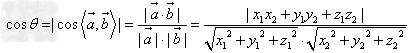 ,
,
(其中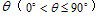 为异面直线a,b所成角,
为异面直线a,b所成角,![]() 分别表示异面直线a,b的方向向量)。
分别表示异面直线a,b的方向向量)。
直线AB与平面所成角:
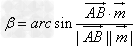 (
( 为平面α的法向量);
为平面α的法向量);
二面角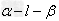 的平面角:
的平面角:
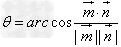 或
或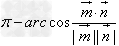 (
(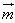 ,
, 为平面α,β的法向量)。
为平面α,β的法向量)。
用向量求异面直线所成角注意:
①求异面直线所成的角常用平移法或向量法,特别是向量法,由于降低了空间想象的要求,所以需引起我们的重视,用向量法时,需注意两异面直线夹角的范围是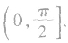
②两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但二者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
求直线与平面所成的角既可选择传统立体几何的综合推理法,也可选择空间向量的向量法:
①求直线和平面所成角的步骤:作出斜线与其射影所成的角;证明所作的角就是要求的角;常在直角三角形(垂线、斜线、射影所组成的直角三角形)中解出所求角的大小:
②在用向量法求直线OP与α所成的角时一般有两种途径:一是直接求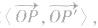 其中OP′,为斜线OP在平面α内的射影;二是通过求
其中OP′,为斜线OP在平面α内的射影;二是通过求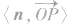 进而转化求解,其中n为平面α的法向量。
进而转化求解,其中n为平面α的法向量。
用向量求二面角注意:
①当法向量 的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于法向量
的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于法向量 的夹角
的夹角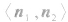 的大小;
的大小;
②当法向量 的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于法向量
的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于法向量 的夹角的补角
的夹角的补角 的大小.
的大小.
求二面角,大致有两种基本方法:
(1)传统立体几何的综合推理法:①定义法;②垂面法;③三垂线定理法;④射影面积法.
(2)空间向量的坐标法:建系并确定点及向量的坐标,分别求出两个平面的法向量,通过求两个法向量的夹角得出二面角的大小.
与“如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为a,(1)建...”考查相似的试题有:
- 若点P(-4,-2,3)关于坐标平面xoy及y轴的对称点的坐标分别是(a,b,c)、(e,f,d),则c与e的和为( ) A.7 B.-7 C.-...
- 如图,在空间直角坐标系中,已知直三棱柱的顶点A在x轴上,AB平行于y轴,侧棱AA1平行于z轴.当顶点C在y轴正半轴上运动时,以下...
- 在空间直角坐标系中,点P(1,,),过点P作平面xOy的垂线PQ,则Q的坐标为A.(0,,0)B.(0,,)C.(1,0,)D.(1,,0)
- 如图所示,正方体的棱长为1,点A是其一棱的中点,则点A在空间直角坐标系中的坐标是( ) A.(,,1) B.(1,1,) C.(,...
- 在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是( )。
- 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.(1)证明:EM⊥BF;(2...
- 已知点H在正方体ABCD-A′B′C′D′的对角线B′D′上,∠HDA=60°.(Ⅰ)求DH与CC′所成角的大小;(Ⅱ)求DH与平面AA′D′D所成角的大小.
- 如图,PA⊥平面ABCD,ABCD为正方形,,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(1)求证:面EFG⊥面PAB;(2)求异面...
- 设A(1,0,0),B(1,0,1),C(0,1,1)D(1,1,1),求直线AD与平面ABC所成的角.
- 平面α的斜线l 与它在这个平面上射影l' 的方向向量分别为 a=(1 ,0 ,1) ,b=(0 ,1 ,1) ,则斜线l 与平面α所成的角为[ ]A.3...