本试题 “某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工...” 主要考查您对简单线性规划问题(用平面区域表示二元一次不等式组)
相互独立事件同时发生的概率
离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 简单线性规划问题(用平面区域表示二元一次不等式组)
- 相互独立事件同时发生的概率
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
二元一次不等式表示的平面区域:
二元一次不等式ax+by+c>0在平面直角坐标系中表示直线ax+by+c=0某一侧所有点组成的平面区域。不等式ax+by+c<0表示的是另一侧的平面区域。
线性约束条件:
关于x,y的一次不等式或方程组成的不等式组称为x,y的线性约束条件;
线性目标函数:
关于x、y的一次式欲达到最大值或最小值所涉及的变量x、y的解析式,叫做线性目标函数;
线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。
可行解、可行域和最优解:
满足线性约束条件的解(x,y)称为可行解;由所有可行解组成的集合称为可行域; 使目标函数取得最大值或最小值的可行解叫做线性规划问题的最优解。
用一元一次不等式(组)表示平面区域:
(1)一般地,直线l:ax+by+c=0把直角坐标平面分成了三个部分:①直线l上的点(x,y)的坐标满足ax+by+c=0;②直线l一侧的平面区域内的点(x,y)的坐标满足ax+by+c>0;③直线l另一侧的平面区域内的点(x,y)的坐标满足ax+by+c<0.所以,只需在直线l的某一侧的平面区域内,任取一特殊点(x0,y0),从ax0+by0+c的值的正负,即可判断不等式表示的平面区域,可简称为,特殊点定域”.
(2)不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
线性规划问题求解步骤:
(1)确定目标函数;
(2)作可行域;
(3)作基准线(z=0时的直线);
(4)平移找最优解;
(5)求最值。
线性规划求最值线性规划求最值问题:
(1)要充分理解目标函数的几何意义,诸如直线的截距、两点间的距离(或平方)、点到直线的距离、过已知两点的直线斜率等.
(2)求最优解的方法①将目标函数的直线平移,最先通过或最后通过的点为最优解,②利用围成可行域的直线的斜率来判断.若围成可行域的直线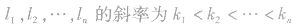 ,且目标函数的斜率k满足
,且目标函数的斜率k满足 的交点一般为最优解.在求最优解前,令z=0的目的是确定目标函数在可行域的什么位置有可行解,值得注意的是,有些问题中可能要求x,y∈N(即整点),它不一定在边界上.特别地,当表示线性目标函数的直线与可行域的某条边平行(
的交点一般为最优解.在求最优解前,令z=0的目的是确定目标函数在可行域的什么位置有可行解,值得注意的是,有些问题中可能要求x,y∈N(即整点),它不一定在边界上.特别地,当表示线性目标函数的直线与可行域的某条边平行(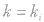 )时,其最优解可能有无数个,用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键.可先将题目的量分类,列出表格,理清头绪,然后列出不等式组(方程组),寻求约束条件,并就题目所述找到目标函数.
)时,其最优解可能有无数个,用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键.可先将题目的量分类,列出表格,理清头绪,然后列出不等式组(方程组),寻求约束条件,并就题目所述找到目标函数.
线性规划的实际应用在线性规划的实际问题中:
主要掌握两种类型:
一、给定一定数量的人力、物力资源,问怎样运用这些资源能使完成的任务量最大,收到的效益最大;
二、给定一项任务,问怎样统筹安排,能使完成这项任务耗费的人力、物力资源最小.
(l)用图解法解决线性规划问题的一般步骤:①分析并将已知数据列出表格;②确定线性约束条件;③确定线性目标函数;④画出可行域;⑤利用线性目标函数(直线)求出最优解;⑥实际问题需要整数解时,应适当调整,以确定最优解.
(2)整数规划的求解,可以首先放松可行解必须为整数的要求,转化为线性规划求解,若所求得的最优解恰为整数,则该解即为整数规划的最优解;若所求得的最优解不是整数,则视所得非整数解的具体情况增加条件;若这两个子问题的最优解仍不是整数,再把每个问题继续分成两个子问题求解,……,直到求出整数最优解为止,
相互独立事件的定义:
如果事件A(或B)是否发生对事件B(A)发生的概率没有影响,这样的两个事件叫做相互独立事件。
若A,B是两个相互独立事件,则A与 ,
, 与
与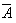 ,
,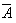 与B都是相互独立事件。
与B都是相互独立事件。
相互独立事件同时发生的概率:
两个相互独立事件同时发生,记做A·B,P(A·B)=P(A)·P(B)。
若A1,A2,…An相互独立,则n个事件同时发生的概率等于每个事件发生的概率的积,即P(A1·A2·…·An)=P(A1)·P(A2)·…·P(An)。
求相互独立事件同时发生的概率的方法:
(1)利用相互独立事件的概率乘法公式直接求解;
(2)正面计算较繁或难以入手时,可从其对立事件入手计算。
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称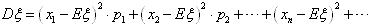 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,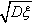 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)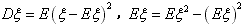 ;
;
(2)若η=aξ+b,则 ;
;
(3)若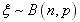 ,则
,则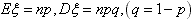 ;
;
(4)若ξ服从几何分布,则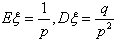 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式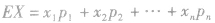 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序...”考查相似的试题有:
- 不等式3x-2y-6>0表示的区域在直线3x-2y-6=0的( )A.右上方B.右下方C.左上方D.左下方
- 不等式组所表示的平面区域图形是[ ]A.第一象限内的三角形B.四边形C.第三象限内的三角形D.以上都不对
- 某射手射击所得环数X的分布列如下:X78910Px0.10.3y已知X的期望E(X)=8.9,则y的值为________.
- 设袋子中装有个红球,个黄球,个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分。(1)当时,从该袋子中...
- 设一随机试验的结果只有和,且,令随机变量,则的方差等于( ) A.m B.2m(1-m) C.m(m-1) D.m(1-m)
- 根据以往资料统计,大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为ζ123P0.40.250.35(1)若事件A={购买该平板...
- (本小题满分12分)甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:射手甲射手乙环数8...
- 现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为、、;已知乙项目的利润与...
- 设随机变量的概率分布为,则的值分别是( ).A.和B.和C.和D.和
- 某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:①每位参加者计分器的初始分均为10分,答对问题A、B、C...