本试题 “若lg(|x-5|+|x+3|)≥1,则x取值范围是______.” 主要考查您对对数函数的图象与性质
绝对值不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数函数的图象与性质
- 绝对值不等式
对数函数的图形:
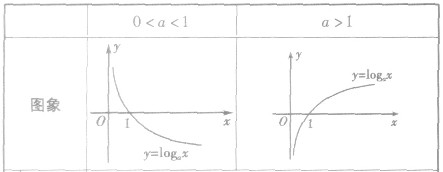
对数函数的图象与性质:
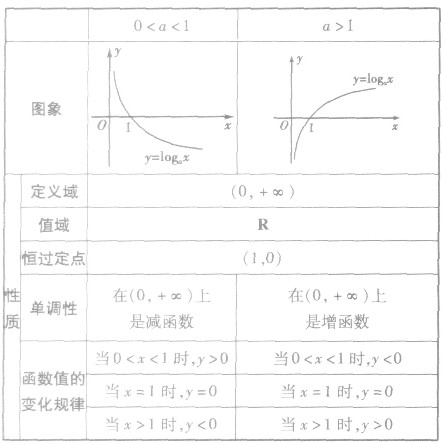
对数函数与指数函数的对比:
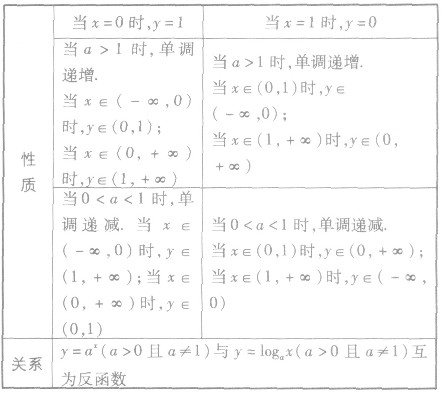
(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,它们是减函数.
(3)指数函数与对数函数的联系与区别: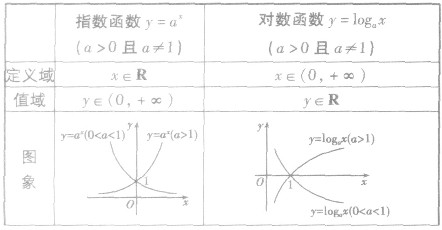
对数函数单调性的讨论:
解决与对数函数有关的函数单调性问题的关键:一是看底数是否大于l,当底数未明确给出时,则应对底数a是否大于1进行讨论;二是运用复合法来判断其单调性,但应注意中间变量的取值范围;三要注意其定义域(这是一个隐形陷阱),也就是要坚持“定义域优先”的原则.
利用对数函数的图象解题:
涉及对数型函数的图象时,一般从最基本的对数函数的图象人手,通过平移、伸缩、对称变换得到对数型函数的图象,特别地,要注意底数a>l与O<a<l的两种不同情况,
底数对函数值大小的影响:
1.在同一坐标系中分别作出函数
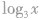 的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
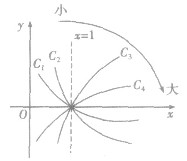
2.类似地,在同一坐标系中分别作出
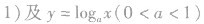 的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如
的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如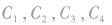 分别对应函数
分别对应函数
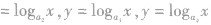 ,则必有
,则必有
绝对值不等式:
当a>0时,有 ;
;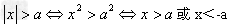 或x<-a 。
或x<-a 。
绝对值不等式的解法:
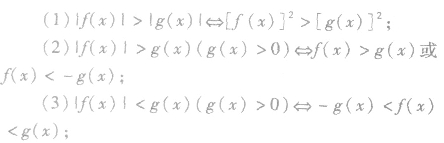
(4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解,也可以用图象法求解。
发现相似题
与“若lg(|x-5|+|x+3|)≥1,则x取值范围是______.”考查相似的试题有:
- log92•(log43+log83).
- 设定义在区间(-b,b)上的函数f(x)=lg1+ax1-2x是奇函数(a,b∈R,且a≠-2),则ab的取值范围是( )A.(1, 2]B.[22, 2]C....
- 已知奇函数f(x)的定义域是{x|x∈R,且x≠0},当x<0时,f(x)=xlg(2-x),求x>0时,f(x)的解析式.
- (1)如果定义在区间(-1,0)的函数f(x)=log3a(x+1)满足f(x)<0,求a的取值范围;(2)解方程:log3(3+2•3x)=2x.
- 函数y=loga(x-1)+2的图象过定点( )A.(3,2)B.(2,1)C.(2,2)D.(2,0)
- 已知函数y=loga(2-ax)在区间[0,1]上是x的减函数,则a的取值范围是[ ]A.(0,1)B.(1,2)C.(0,2)D.(2,+∞)
- 已知f(x)=loga1+x1-x,(a>0,a≠1)(1)求f(x)的定义域;(2)证明f(x)的图象关于原点对称(3)求使f(x)>0的x取值范围.
- 不等式的解集为( )A.B.C.D.
- 不等式的解集为______________________________.
- 不等式|2x-a|<2的解为1<x<3,则a=______.