直线与圆的位置关系：

由直线与圆的公共点的个数，得出以下直线和圆的三种位置关系：
（1）相交：直线与圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线。
（2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，唯一的公共点叫做切点。
（3）相离：直线和圆没有公共点时，叫做直线和圆相离。
其图像如下：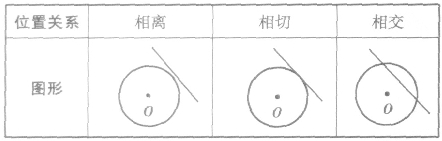

直线和圆的位置关系的性质：

（1）直线l和⊙O相交d＜r
（2）直线l和⊙O相切d=r；
（3）直线l和⊙O相离d＞r。

直线与圆位置关系的判定方法：

(1)代数法:判断直线Ax+By+C=0和圆x²+y²+Dx+Ey+F=0的位置关系，可由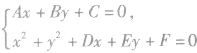
 
推出mx²+nx+p=0，利用判别式△进行判断．
△>0则直线与圆相交；
△=0则直线与圆相切；
△<0则直线与圆相离．
(2)几何法:已知直线Ax+By+C=0和圆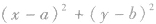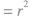，圆心到直线的距离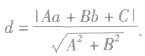
d<r则直线和圆相交；
d=r则直线和圆相切；
d>r则直线和圆相离．
特别提醒:
(1)上述两种方法，以利用圆心到直线的距离进行判定较为简捷，而判别式法也适用于直线与椭圆、双曲线、抛物线位置关系的判断．
(2)直线与圆相交，应抓住半径、弦心距、半弦长组成的直角三角形，可使解法简单.

直线与圆位置关系的判定方法列表如下：

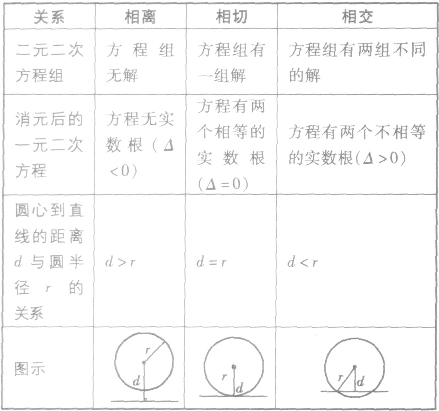
直线与圆相交的弦长公式：

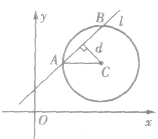
（1）几何法：如图所示，直线l与圆C相交于A、B两点，线段AB的长即为l与圆相交的弦长。
设弦心距为d，半径为r，弦为AB，则有|AB|=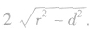

（2）代数法：直线l与圆交于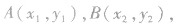直线l的斜率为k，则有
当直线AB的倾斜角为直角，即斜率不存在时，|AB|=

圆与圆的位置关系：

圆与圆有五种位置关系：相交、外离、外切、内切和内含。

圆与圆的位置关系的判断方法：

（1）利用圆心距和两圆半径比较大小（几何法）已知两圆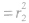的圆心距为d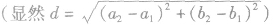，则位置关系表示如下：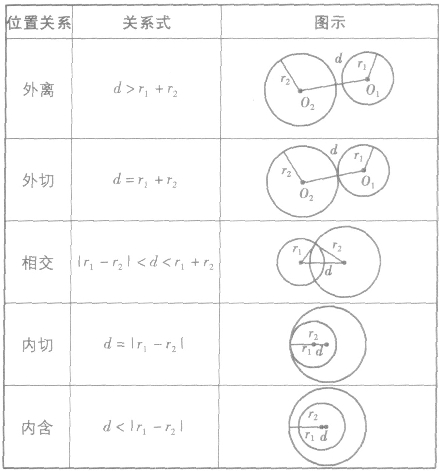

（2）利用两圆的交点进行判断（代数法）
设由两圆的方程组成的方程组为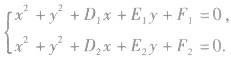
 
由此方程组得：有两组不同的实数解则两圆相交；有两组相同的实数解则两圆相切；无实数解则两圆相离．

两圆公切线条数的确定：

两圆的公切线的条数是由两圆的位置关系确定的，设两圆的圆心距为d，两圆的半径分别为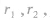
则当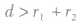时，两圆外离，此时有四条公切线；
当时，两圆外切，连心线过切点，此时有三条公切线，有外公切线两条，内公切线一条；
当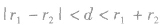时，两圆相交，连心线垂直平分公共弦，有两条外公切线；
当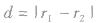时，两圆内切，连心线过切点，此时只有一条公切线；
当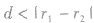时，两圆内含，此时没有公切线。