本试题 “符号[x]表示不超过x的最大整数,如[π]=3,[-1.08]=-2,定义函数{x}=x-[x].给出下四个命题:①函数{x}的定义域是R,值域为[0,1]②方程{x}=12有无数个解;③函数...” 主要考查您对函数、映射的概念
函数的定义域、值域
函数图象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数、映射的概念
- 函数的定义域、值域
- 函数图象
1、映射:
(1)设A,B是两个非空集合,如果按照某一个确定的对应关系f,使对于集合A中的任何一个元素x,在集合B中都有唯一确定的元素y与之对应,
那么,就称对应f:A→B为从集合A到集合B的映射,记作:f:A→B。
(2)像与原像:如果给定一个集合A到集合B的映射,那么,和集合A中的a对应的集合B中的b叫做a的像,a叫做b的原像。
2、函数:
(1)定义(传统):如果在某变化过程中有两个变量x,y并且对于x在某个范围内的每一个确定的值,按照某个对应法则,y都有唯一确定的值和它对应,那么y就是x的函数,x叫做自变量,x的取值范围叫做函数的定义域,和x的值对应的y的值叫做函数值,函数值的集合叫做函数的值域。
(2)函数的集合定义:设A,B都是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任何一个元素x,在集合B中都有唯一确定的数f(x)和它对应,那么就称
f:x→y为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中,x叫做自变量,x的取值范围A叫做函数f(x)的定义域,与x的值相对应的y值叫做函数值,函数值的集合{ f(x)|x∈A}叫做函数f(x)的值域。显然值域是集合B的子集。
3、构成函数的三要素:
定义域,值域,对应法则。
值域可由定义域唯一确定,因此当两个函数的定义域和对应法则相同时,值域一定相同,它们可以视为同一函数。
4、函数的表示方法:
(1)解析法:如果在函数y=f(x)(x∈A)中,f(x)是用代数式(或解析式)来表达的,则这种表示函数的方法叫做解析式法;
(2)列表法:用表格的形式表示两个量之间函数关系的方法,称为列表法;
(3)图象法:就是用函数图象表示两个变量之间的关系。
注意:函数的图象可以是一个点,或一群孤立的点,或直线,或直线的一部分,或若干曲线组成。
映射f:A→B的特征:
(1)存在性:集合A中任一a在集合B中都有像;
(2)惟一性:集合A中的任一a在集合B中的像只有一个;
(3)方向性:从A到B的映射与从B到A的映射一般是不一样的;
(4)集合B中的元素在集合A中不一定有原象,若集合B中元素在集合A中有原像,原像不一定惟一。
(1)函数两种定义的比较:
①相同点:1°实质一致2°定义域,值域意义一致3°对应法则一致
②不同点:1°传统定义从运动变化观点出发,对函数的描述直观,具体生动.
2°近代定义从集合映射观点出发,描述更广泛,更具有一般性.
(2)对函数定义的更深层次的思考:
映射与函数的关系:函数是一种特殊的映射f:A→B,其特殊性表现为集合A,B均为非空的数集. .函数:AB是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与轴的垂线至多有一个公共点,但与轴垂线的公共点可能没有,也可能有任意个。小结:函数概念8个字:非空数集上的映射。
对于映射这个概念,应明确以下几点:
①映射中的两个集合A和B可以是数集,点集或由图形组成的集合以及其它元素的集合.
②映射是有方向的,A到B的映射与B到A的映射往往是不相同的.
③映射要求对集合A中的每一个元素在集合B中都有象,而这个象是唯一确定的.这种集合A中元素的任意性和在集合B中对应的元素的唯一性构成了映射的核心.
④映射允许集合B中的某些元素在集合A中没有原象,也就是由象组成的集合 .
.
⑤映射允许集合A中不同的元素在集合B中有相同的象,即映射只能是“多对一”或“一对一”,不能是“一对多”.
一一映射:设A,B是两个集合,f:A→B是从集合A到集合B的映射,如果在这个映射的作用下,对于集合A中的不同的元素,在集合B中有不同的象,而且B中每一元素都有原象,那么这个映射叫做从A到B上的一一映射. 一一映射既是一对一又是B无余的映射.
在理解映射概念时要注意:⑴A中元素必须都有象且唯一; ⑵B中元素不一定都有原象,但原象不一定唯一。总结:取元任意性,成象唯一性。
对函数概念的理解:
函数三要素
(1)核心——对应法则等式y=f(x)表明,对于定义域中的任意x,在“对应法则f”的作用下,即可得到y.因此,f是使“对应”得以实现的方法和途径.是联系x与y的纽带,从而是函数的核心.对于比较简单的函数,对应法则可以用一个解析式来表示,但在不少较为复杂的问题中,函数的对应法则f也可以采用其他方式(如图表或图象等).
(2)定义域定义域是自变量x的取值范围,它是函数的一个不可缺少的组成部分,定义域不同而解析式相同的函数,应看作是两个不同的函数. 在中学阶段所研究的函数通常都是能够用解析式表示的.如果没有特别说明,函数的定义域就是指能使这个式子有意义的所有实数x的集合.在实际问题中,还必须考虑自变量所代表的具体的量的允许取值范围问题.
(3)值域值域是全体函数值所组成的集合.在一般情况下,一旦定义域和对应法则确定,函数的值域也就随之确定.因此,判断两个函数是否相同,只要看其定义域与对应法则是否完全相同,若相同就是同一个函数,若定义域和对应法则中有一个不同,就不是同一个函数. 同一函数概念。构成函数的三要素是定义域,值域和对应法则。而值域可由定义域和对应法则唯一确定,因此当两个函数的定义域和对应法则相同时,它们一定为同一函数。
(4)关于函数符号y=f(x)
1°、y=f(x)即“y是x的函数”这句话的数学表示.仅仅是函数符号,不是表示“y等于f与x的乘积”.f(x)也不一定是解析式.
2°、f(x)与f(a)的区别:f(x)是x的函数,在通常情况下,它是一个变量.f(a)表示自变量x=a时所得的函数值,它是一个常量即是一个数值.f(a)是f(x)的一个当x=a时的特殊值.
3°如果两个函数的定义域和对应法则相同虽然表示自变量的与函数的字母不相同,那么它们仍然是同一个函数,但是如果定义域与对应法则中至少有一个不相同,那么它们就不是同一个函数.
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则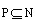 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如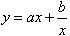 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
定义:
点集{(x,y)|y=f(x)}叫做函数y=f(x)的图像。
函数图像的画法:
(1)描点法:
一般我们选择一些特殊点(包括区间端点、最值点、极值点、函数图像与坐标轴的交点等)。
(2)用函数的性质画图
一般我们选择先确定函数的定义域,再看函数是否具有周期性和对称性、奇偶性,这样我们就可以只画出部分图像,之后根据性质直接得到其余部分的图像,然后判断单调性,确定特殊点或渐近线,进而得到函数的大致图像。
(3)通过图像变换画图
(一)平移变化:
Ⅰ水平平移:函数y=f(x+a)的图像可以把函数y=f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位即可得到;
Ⅱ竖直平移:函数y=f(x+a)的图像可以把函数y=f(x)的图像沿x轴方向向上(a>0)或向下(a<0)平移|a|个单位即可得到.
(二)对称变换:
Ⅰ函数y=f(-x)的图像可以将函数y=f(x)的图像关于y轴对称即可得到;
Ⅱ函数y=-f(x)的图像可以将函数y=f(x)的图像关于x轴对称即可得到;
Ⅲ函数y=-f(-x)的图像可以将函数y=f(x)的图像关于原点对称即可得到;
Ⅳ函数y=f-1(x)的图像可以将函数y=f(x)的图像关于直线y=x对称得到.
函数图像的判断:
这里主要是抽象函数的图像,借助函数的对称性、周期性及单调性确定函数的图像;另外借助导数,就是函数在某点处的切线斜率的变化,体现在函数的图像上就是增长的快还是慢来确定函数的图像。
常用结论:
(1)若函数y=f(x)定义域内任一x的值都满足f(a+x)=f(b-x),则y=f(x)的图像关于直线 成轴对称图形;特别地,y=f(x)满足
成轴对称图形;特别地,y=f(x)满足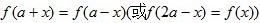 恒成立,则y=f(x)的图像关于直线x=a成轴对称图形;
恒成立,则y=f(x)的图像关于直线x=a成轴对称图形;
(2)函数y=f(x)的图像关于直线x=a及x=b对称,则y=f(x)是周期函数,且2|b-a|是它的一个周期。
与“符号[x]表示不超过x的最大整数,如[π]=3,[-1.08]=-2,定义函...”考查相似的试题有:
- (本题14分)已知函数,(Ⅰ) 设函数f(x)的图象与x轴交点为A, 曲线y=f(x)在A点处的切线方程是, 求的值;(Ⅱ) 若函数, 求函数的单调...
- 关于的方程(为自然对数的底数)有唯一解,则的取值范围是( )A.B.C.或D.
- 函数的定义域为,若,,则( )A.B.C.D.
- 函数是定义在R上的偶函数,当时,,那么当时,的解析式是 A.B.C.D.
- 对于实数,符号表示不超过的最大整数,例如,定义函数,则下列命题中正确的是( )A.B.方程有且仅有一个解C.函数是周期函数D.函...
- 已知函数是定义在上的奇函数,且当时,不等式成立,若,,,则a,b,c间的大小关系是( ).A.a>b>cB.c>b>aC.c>a>bD....
- 下列函数中,与函数y=x -12有相同定义域的是( )A.y=exB.y=lnxC.y=1xD.y=|x|
- 函数y=的定义域为[ ]A.(﹣B.C.D.
- 函数的单调增区间为 .
- 函数的图象大致是[ ]A、B、C、D、