本试题 “一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10公里的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问(1)若轮...” 主要考查您对指数函数模型的应用
对数函数模型的应用
函数的最值与导数的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数函数模型的应用
- 对数函数模型的应用
- 函数的最值与导数的关系
恰当选择自变量将问题的目标表示成自变量的函数f(x)=a·bx+c(a、b、c为常数,a≠0,b>0,b≠1)的形式,进而结合指数函数的性质解决问题。
指数型复合函数的性质的应用:
(1)与指数函数有关的复合函数基本上有两类:![]() ;②
;②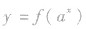 .无论是哪一类,要搞清楚复合过程,才能确定复合函数的值域和单调区间,具体问题中,a的取值不定时,要对a进行分类讨论.
.无论是哪一类,要搞清楚复合过程,才能确定复合函数的值域和单调区间,具体问题中,a的取值不定时,要对a进行分类讨论.
(2)对于形如![]() 一类的指数型复合函数,有以下结论:
一类的指数型复合函数,有以下结论:
①函数 的定义域与f(x)的定义域相同;
的定义域与f(x)的定义域相同;
②先确定函数f(x)的值域,再根据指数函数的值域、单调性,确定函数 的值域;
的值域;
③当a>l时,函数 与函数f(x)的单调性相同;当O<a<l时,函数
与函数f(x)的单调性相同;当O<a<l时,函数 与函数f(x)的单调性相反.
与函数f(x)的单调性相反.
对数函数模型的定义:
恰当选择自变量将问题的目标表示成自变量的函数f(x)=mlogax+n(m、n、a为常数,m≠0,a>0,a≠1)的形式,进而结合对数函数的性质解决问题。
对数函数模型解析式:
f(x)=mlogax+n(m、n、a为常数,m≠0,a>0,a≠1)
用函数模型解函数应用题的步骤:
1.审题:弄清题意,分清条件和结论,确定数量关系,初步选择数学模型;
2.建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;
3.求模:求解数学模型,得出数学结论;
4.还原:将数学问题还原为实际问题的意义。
函数的最大值和最小值:
在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值,分别对应该区间上的函数值的最大值和最小值。
利用导数求函数的最值步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a)、f(b)比较得出函数f(x)在[a,b]上的最值。
用导数的方法求最值特别提醒:
①求函数的最大值和最小值需先确定函数的极大值和极小值,因此,函数极大值和极小值的判别是关键,极值与最值的关系:极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值;
②如果仅仅是求最值,还可将上面的办法化简,因为函数fx在[a,b]内的全部极值,只能在f(x)的导数为零的点或导数不存在的点取得(下称这两种点为可疑点),所以只需要将这些可疑点求出来,然后算出f(x)在可疑点处的函数值,与区间端点处的函数值进行比较,就能求得最大值和最小值;
③当f(x)为连续函数且在[a,b]上单调时,其最大值、最小值在端点处取得。
生活中的优化问题:
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题,解决优化问题的方法很多,如:判别式法,均值不等式法,线性规划及利用二次函数的性质等,
不少优化问题可以化为求函数最值问题.导数方法是解这类问题的有效工具.
用导数解决生活中的优化问题应当注意的问题:
(1)在求实际问题的最大(小)值时,一定要考虑实际问题的意义,不符合实际意义的值应舍去;
(2)在实际问题中,有时会遇到函数在区间内只有一个点使f'(x)=0的情形.如果函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值;
(3)在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定出函数关系式中自变量的定义区间.
利用导数解决生活中的优化问题:
(1)运用导数解决实际问题,关键是要建立恰当的数学模型(函数关系、方程或不等式),运用导数的知识与方法去解决,主要是转化为求最值问题,最后反馈到实际问题之中.
(2)利用导数求f(x)在闭区间[a,b]上的最大值和最小值的步骤,
①求函数y =f(x)在(a,b)上的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(3)定义在开区间(a,b)上的可导函数,如果只有一个极值点,该极值点必为最值点.
与“一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已...”考查相似的试题有:
- 2010年某电视生产厂家中标商务部家电下乡活动,若厂家投放A、B型号电视机的价值分别为p万元,q万元,农民购买电视机获得的补...
- 当a>0且a≠1时,函数f(x)=ax-2-3必过定点
- 不论a为何值时,函数y=(a-1)•2x-2a恒过一定点,这个定点坐标是______.
- 若函数是定义在上的偶函数,在上是减函数,且,则使得的x的取值范围是 ( )
- 在边长为30cm的正方形纸板的四角剪去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底盒子,盒子的底面边长...
- 经市场调查,某种商品在120天内的日销售量和售价均为时间t(天)的函数,日销售量与时间的关系用图(1)的一条折线表示,售价...
- 设函数f(x)=x2-alnx与g(x)=1ax-x的图象分别交直线x=1于点A,B,且曲线y=f(x)在点A处的切线与曲线y=g(x)在点B处的切线平...
- 设函数f(x)=xsinx在x=x0处取得极值,则(1+x02)cos2x0的值为( ) A.0 B.1 C.2 D.3
- 已知f(x)=ax-lnx,x∈(0,e)其中e是自然常数,a∈R.(1)讨论a=1时,f(x)的单调性、极值;(2)是否存在实数a,使f(x)...
- 已知函数f(x)=sinx-x,x∈[0,π],cosx0=(x0∈[0,π]),那么下面结论正确的是[ ]A.f(x)在[0,x0]上是减函数B.f(x)在[x0,π]上...