返回

高中数学

首页
首页 高中数学知识 函数的奇偶性、周期性 数列求和的其他方法（倒序相加，错位相减，裂项相加等） 平面向量的应用 试题正文
  • 解答题
    在平面直角坐标系xOy中，点An满足
    OA1
    =(0，1)    ，且
    AnAn+1
    =(1，1)    ；点Bn满足
    OB1
    =(3，0)    ，且
    BnBn+1
    =(3•(
    2
    3
    )n，0)    ，其中n∈N*．
    （1）求
    OA2
    的坐标，并证明点An在直线y=x+1上；
    （2）记四边形AnBnBn+1An+1的面积为an，求an的表达式；
    （3）对于（2）中的an，是否存在最小的正整数P，使得对任意n∈N*都有an＜P成立？若存在，求P的值；若不存在，请说明理由．
    本题信息：2013年普陀区一模数学解答题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “在平面直角坐标系xOy中，点An满足OA1=(0，1)，且AnAn+1=(1，1)；点Bn满足OB1=(3，0)，且BnBn+1=(3•(23)n，0)，其中n∈N*．（1）求OA2的坐标，并证明点An在直线...” 主要考查您对

函数的奇偶性、周期性

数列求和的其他方法（倒序相加，错位相减，裂项相加等）

平面向量的应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 函数的奇偶性、周期性
  • 数列求和的其他方法（倒序相加，错位相减，裂项相加等）
  • 平面向量的应用

函数的奇偶性定义：

偶函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），则称函数f（x）为偶函数。
奇函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）＝-f（x），那么函数f（x）是奇函数。 
 
函数的周期性：

（1）定义：若T为非零常数，对于定义域内的任一x，使f（x+T）=f（x）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。
周期函数定义域必是无界的。
（2）若T是周期，则k·T（k≠0，k∈Z）也是周期，所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期，如常函数f（x）=C。


奇函数与偶函数性质：

（1）奇函数与偶函数的图像的对称性：奇函数的图像关于原点对称，偶函数的图像关于y轴对称。
（3）在公共定义域内，①两个奇函数的和是奇函数，两个奇函数的积是偶函数； ②两个偶函数的和、积是偶函数； ③一个奇函数，一个偶函数的积是奇函数。

注：定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．


1、函数是奇函数或偶函数的前提定义域必须关于原点对称；定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．

2、函数的周期性    令a , b 均不为零，若： 
（1）函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a| 
（2）函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a| 
（3）函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a| 
（4）函数y = f(x) 存在 f(x + a) =  ==> 函数最小正周期 T=|2a| 
（5）函数y = f(x) 存在 f(x + a) = 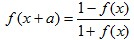  ==> 函数最小正周期 T=|4a|


数列求和的常用方法：

1.裂项相加法：数列中的项形如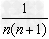的形式，可以把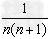表示为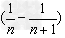，累加时抵消中间的许多项，从而求得数列的和；
2、错位相减法：源于等比数列前n项和公式的推导，对于形如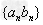的数列，其中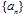为等差数列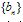，为等比数列，均可用此法；
3、倒序相加法：此方法源于等差数列前n项和公式的推导，目的在于利用与首末两项等距离的两项相加有公因式可提取，以便化简后求和。
4、分组转化法：把数列的每一项分成两项，或把数列的项“集”在一块重新组合，或把整个数列分成两个部分，使其转化为等差或等比数列，这一求和方法称为分组转化法。
5、公式法求和：所给数列的通项是关于n的多项式，此时求和可采用公式求和，常用的公式有：
 
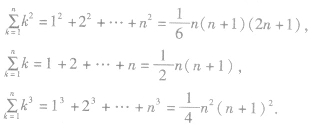
数列求和的方法多种多样，要视具体情形选用合适方法。


数列求和特别提醒：

（1）对通项公式含有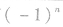的一类数列，在求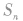时，要注意讨论n的奇偶性；
（2）在用等比数列前n项和公式时，一定要分q=1和q≠1两种情况来讨论。

 

平面向量在几何、物理中的应用

1、向量在平面几何中的应用：
（1）证明线段相等平行，常运用向量加法的三角形法则、平行四边形法则，有时也用到向量减法的定义；
（2）证明线段平行，三角形相似，判断两直线（或线段）是否平行，常运用到向量共线的条件；
（3）证明垂直问题，常用向量垂直的充要条件；
1、向量在三角函数中的应用：
（1）以向量为载体研究三角函数中最值、单调性、周期等三角函数问题；
（2）通过向量的线性运算及数量积、共线来解决三角形中形状的判断、边角的大小与关系。
2、向量在物理学中的应用：
由于力、速度是向量，它们的分解与合成与向量的加法相类似，可以用向量方法来解决，力做的功就是向量中数量积的一种体现。
3、向量在解析几何中的应用：
（1）以向量为工具研究平面解析几何中的坐标、性质、长度等问题；
（2）以向量知识为工具研究解析几何中常见的轨迹与方程问题。


平面向量在几何、物理中的应用

1、用向量解决几何问题的步骤：
（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面问题转化为向量问题；
（2）通过向量运算，研究几何元素之间的关系，如：距离，夹角等；
（3）把运算结果“翻译”成几何关系。
2、用向量中的有关知识研究物理中的相关问题，步骤如下：
（1）问题的转化，即把物理问题转化为数学问题；
（2）模型的建立，即建立以向量为主题的数学模型；
（3）求出数学模型的有关解；
（4）将问题的答案转化为相关的物理问题。


发现相似题
与“在平面直角坐标系xOy中，点An满足OA1=(0，1)，且AnAn+1=(1，1...”考查相似的试题有：