本试题 “在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且...” 主要考查您对正弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即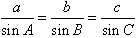 =2R。
=2R。
有以下一些变式:
(1)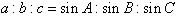 ;
;
(2)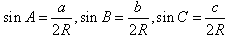 ;
;
(3)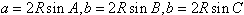 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 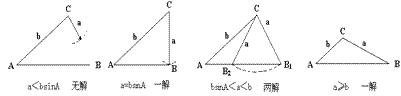
也可根据a,b的关系及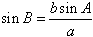 与1的大小关系来确定。
与1的大小关系来确定。
发现相似题
与“在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒...”考查相似的试题有:
- 已知O是平面上的一定点,A,B,C是平面上不共线的三点,动点P满足,,则动点P的轨迹一定通过的( )A.重心B.垂心C.外心D....
- 在中,角,,的对边为,,且;(Ⅰ)求的值;(Ⅱ)若,,求的值.
- 在△ABC中,已知内角A=π3,边BC=23.设内角B=x,△ABC的面积为y.(Ⅰ)求函数y=f(x)的解析式和定义域;(Ⅱ)当角B为何值时,△...
- 已知圆A的直径为23,圆B的直径为4-23,圆C的直径为2,圆A与圆B外切,圆A又与圆C外切∠A=60°,求BC及∠C.
- 已知a,b,c,分别是△ABC的三个内角A,B,C的对边,且acosA=bcosB,则△ABC一定是( ) A.等腰三角形 B.直角三角形 C.等边...
- 在△ABC中,a=80,b=100,A=30°,则三角形的解的个数是( )A.0个B.1个C.2个D.不确定
- 在△ABC中,角A,B,C所对的边分别为a,b,c,若a=6,b=3,B=60°,则A的度数为______.
- 在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsinA=3csinB,a=3,cosB=(1)求b的值;(2)求sin的值.
- (本小题满分10分)在中,分别为角所对的三边,已知.(Ⅰ)求角的值;(Ⅱ)若,,求的长.
- 在中,角A、B、C所对的边分别为、、.已知向量,,且.(Ⅰ) 求角的大小;(Ⅱ) 若,求边的最小值.