本试题 “已知a,b,c是同一平面内的三个向量,其中a=(1, 2).(Ⅰ)若|b|=35,且b∥a,求b的坐标;(Ⅱ)若c与a的夹角θ的余弦值为-510,且(a+c)⊥(a-9c),求|c|.” 主要考查您对用数量积表示两个向量的夹角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
用数量积表示两个向量的夹角:
设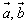 都是非零向量,
都是非零向量,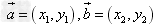 ,θ是
,θ是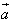 与
与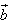 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得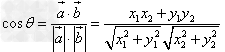 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
发现相似题
与“已知a,b,c是同一平面内的三个向量,其中a=(1, 2).(Ⅰ)若...”考查相似的试题有:
- 设0<|a|≤2,函数f(x)=cos2x-|a|sinx-|b|的最大值0,最小值为-4,且a与b的夹角为45°,求(a+b)2.
- 与向量的夹角相等,且模为1的向量是[ ]A、B、或C、D、或
- 平面直角坐标系中,已知A(1,2),B(2,3).(I)求|AB|的值;(Ⅱ)设函数f(x)=x2+1的图象上的点C(m,f(m))使∠CAB为...
- 已知向量a,b满足(a+2b)•(a-b)=-6,|a|=1,|b|=2,则a与b的夹角为______.
- 如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤π2)的图象与y轴交与点(0,1).(1)求φ的值;(2)设P是图象上的最高点,M,N是...
- 已知O为坐标原点,OA=(-3,1),OB=(0,5),且AC∥OA,BC⊥AB,则点C的坐标为______.
- 已知向量a=(1,1),b=(2,3),则向量a与2a-b的夹角为______.
- 已知|a|=3,|b|=8且a与b的夹角为120°,则a在b方向上的投影为( )A.4B.32C.-32D.-4
- |a|=4,|b|=5,|a-b|=41-203,则a,b的夹角的大小为 ______.
- 设a、b为两非零向量,且满足|a|+|b|=2,2a•b=a2•b2,则两向量a、b的夹角的最小值为______.