本试题 “已知向量a=(1,-2),b=(x,y),若x,y∈[1,4],则满足a•b>0的概率为______.” 主要考查您对向量数量积的运算
几何概型的定义及计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的运算
- 几何概型的定义及计算
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量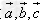 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)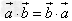 ;
;
(2)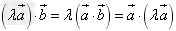 ;
;
(3)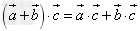 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
几何概型的概念:
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)称比例,则称这样的概率模型为几何概率模型,简称为几何概型。
几何概型的概率:
一般地,在几何区域D中随机地取一点,记事件"该点落在其内部一个区域d内"为事件A,则事件A发生的概率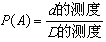 。
。
说明:(1)D的测度不为0;
(2)其中"测度"的意义依D确定,当D分别是线段,平面图形,立体图形时,相应的"测度"分别是长度,面积和体积;
(3)区域为"开区域";
(4)区域D内随机取点是指:该点落在区域内任何一处都是等可能的,落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关.
几何概型的基本特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等.
发现相似题
与“已知向量a=(1,-2),b=(x,y),若x,y∈[1,4],则满足a•b...”考查相似的试题有:
- 设F1、F2分别是椭圆的左、右焦点.(Ⅰ)若P是该椭圆上的一个动点,求PF1●PF2的最大值和最小值;(Ⅱ)设过定点M(0,2)的直线...
- 在极坐标系中,圆与直线交于A,B两点,O为极点,则( )
- 已知且满足.(1)求函数y=f(x)的解析式及最小正周期;(2)在锐角三角形ABC中,若,且AB=2,AC=3,求BC的长.
- 已知双曲线的焦点为F1、F2,点M在双曲线上且,则点M到x轴的距离为( )A.B.C.D.
- 在△ABC中,,.(Ⅰ)求角A;(Ⅱ)设△ABC的面积为S,且,求边AC的长.
- 已知m=(3sinx,cosx),n=(cosx,-cosx),x∈R,定义函数f(x)=m•n-12(1)求函数f(x)的最小正周期,值域,单调增区间....
- 在ΔABC中,a=5,b=8,C=60°,则A.20B.-20C.20D.-20
- 在区间之间随机抽取一个数,则 满足的概率为( )A.B.C.D.
- 如图所示的“赵爽弦图”中,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角,现...
- 在Rt△ABC中,∠A=90°,AB=1,BC=2,在BC边上任取一点M,则∠AMB≥90°的概率为( )。