返回

高中二年级数学

首页
首页 高中二年级数学知识 集合间的基本关系 试题正文
  • 单选题
    设集合A={x||x-a|＜1，x∈R} ，B={x||x-b|＞2，x∈R}，若AB，则实数a，b必满足

    [     ]


    A.|a+b|≤3
    B.|a+b|≥3
    C.|a-b|≤3
    D.|a-b|≥3


    本题信息：2011年期末题数学单选题难度一般 来源:张玲玲
  • 本题答案
    查看答案
本试题 “设集合A={x||x-a|＜1，x∈R} ，B={x||x-b|＞2，x∈R}，若AB，则实数a，b必满足[ ]A.|a+b|≤3B.|a+b|≥3C.|a-b|≤3D.|a-b|≥3” 主要考查您对

集合间的基本关系

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 集合间的基本关系

集合与集合的关系有“包含”与“不包含”，“相等”三种：

 1、 子集概念：
一般地，对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，就说集合B包含A，记作A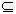B（或说A包含于B），
也可记为B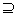A（B包含A），此时说A是B的子集；A不是B的子集，记作A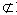B，读作A不包含于B

2、集合相等：
对于集合A和B，如果集合A中的每一个元素都是集合B的元素，反过来，集合B的每一个元素也都是集合A的元素，即集合A是集合B的子集，且集合B是集合A的子集，我么就说集合A和集合B相等，记作A=B

3、真子集：
对于集合A与B，如果A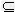B并且A≠B，则集合A是集合B的真子集，记作AB（B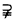A），读作A真包含于B（B真包含A） 


集合间基本关系：

性质1：

（1）空集是任何集合的子集，即A；

（2）空集是任何非空集合的真子集；

（3）传递性：AB，BCAC；AB，BCAC；

（4）AB，BAA=B。

性质2：

 子集个数的运算：含n个元素的集合A的子集有2n个，非空子集有2n-1个，非空真子集有2n-2个。


集合间基本关系性质：

（1）空集是任何集合的子集，即A；
（2）空集是任何非空集合的真子集；
（3）传递性：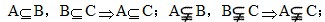 
（4）集合相等： 
（5）含n个元素的集合A的子集有2n个，非空子集有2n-1个，非空真子集有2n-2个。


发现相似题
与“设集合A={x||x-a|＜1，x∈R} ，B={x||x-b|＞2，x∈R}，若AB，则...”考查相似的试题有：