返回

高中数学

首页
首页 高中数学知识 定积分的概念及几何意义 定积分的简单应用 试题正文
  • 单选题
    下列表示图中f（x）在区间[a，b]上的图象与x轴围成的面积总和的式子中，正确的是（　　）
    魔方格
    A．
    ∫ba
    f(x)dx
    B．|
    ∫ba
    f(x)dx    |
    C．
    ∫c1a
    f(x)dx+
    ∫c2c1
    f(x)dx+
    ∫c
    c 2
    f(x)dx
    D．
    ∫c1a
    f(x)dx-
    ∫c2c1
    f(x)dx+
    ∫cc2
    f(x)dx

    本题信息：数学单选题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “下列表示图中f（x）在区间[a，b]上的图象与x轴围成的面积总和的式子中，正确的是（ ）A．∫baf(x)dxB．|∫baf(x)dx|C．∫c1af(x)dx+∫c2c1f(x)dx+∫cc 2f(x)dxD．∫...” 主要考查您对

定积分的概念及几何意义

定积分的简单应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 定积分的概念及几何意义
  • 定积分的简单应用

定积分的定义：

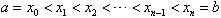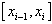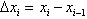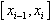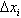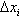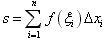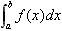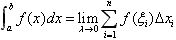设函数f（x）在[a，b]上有界（通常指有最大值和最小值），在a与b之间任意插入n-1个分点，，将区间[a，b]分成n个小区间（i=1，2，…，n），记每个小区间的长度为（i=1，2，…，n），在上任取一点ξi，作函数值f（ξi）与小区间长度的乘积f（ξi） （i=1，2，…，n），并求和，记λ=max{△xi；i=1，2，…，n }，如果当λ→0时，和s总是趋向于一个定值，则该定值便称为函数f(x)在[a，b]上的定积分，记为，即，其中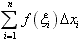， 称为函数f(x)在区间[a，b]的积分和。

定积分的几何意义：

定积分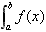在几何上，
当f（x）≥0时，表示由曲线y=f（x）、直线x=a、直线x=b与x轴所围成的曲边梯形的面积；
当f（x）≤0时，表示由曲线y=f（x）、直线x=a、直线x=b与x轴所围成的曲边梯形的面积的负值；
一般情况下，表示介于曲线y=f（x）、两条直线x=a、x=b与x轴之间的个部分面积的代数和。


定积分的性质：

（1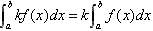）（k为常数）；
（2）；
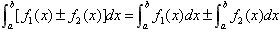（3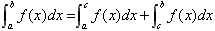）（其中a＜c＜b）。


 定积分特别提醒：

①定积分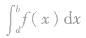不是一个表达式，而是一个常数，它只与被积函数及积分区间有关，而与积分变量的记法无关，例如：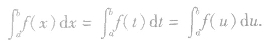 
②定义中区间的分法和ξ的取法是任意的，


定积分的简单应用：

1、求几何图形的面积：在直角坐标系中，由曲线f(x)，直线x=a，x=b(a<b)和x轴围成的曲边梯形的面积，当对应的曲边梯形位于x轴上方时，定积分的取值为正值；当对应的曲边梯形位于x轴下方时，定积分的取值为负值；当位于x轴上方的曲边梯形面积等于位于x轴下方的曲线梯形面积时，定积分的值为0．
2、变速运动问题：如果变速运动的物体的速度v关于时间t的函数是v=v(t)(v(t)≥0)，那么物体从时刻t=a到t=b所经过的路程为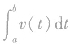如果变速运动的物体的速度v关于时间t的函数是v=v(t)
(v(t）≤0)，那么物体从时刻t=a到t=b所经过的路程为。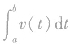


求定积分的方法：

方法1：用定义求定积分的一般步骤：
    (1)分割：n等分区间[a，b]；
    (2)近似代替：取点ξi∈[xi-1，xi]；
    (3)求和:
    (4)取极限:

方法2：用所求定积分表示的几何意义求积分
当定积分表示的面积容易求时，则利用定积分的几何意义求积分.


发现相似题
与“下列表示图中f（x）在区间[a，b]上的图象与x轴围成的面积总和...”考查相似的试题有：