本试题 “已知双曲线与圆交于A、B、C、D四点,若四边形ABCD是正方形,则双曲线的离心率是[ ]A.B.C.D.” 主要考查您对圆的标准方程与一般方程
双曲线的性质(顶点、范围、对称性、离心率)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 圆的标准方程与一般方程
- 双曲线的性质(顶点、范围、对称性、离心率)
圆的定义:
平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心,定长就是半径。
圆的标准方程:
圆的标准方程 ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为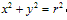 。
。
圆的一般方程:
圆的一般方程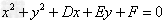
当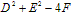 >0时,表示圆心在
>0时,表示圆心在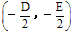 ,半径为
,半径为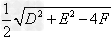 的圆;
的圆;
当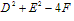 =0时,表示点
=0时,表示点 ;
;
当 <0时,不表示任何图形。
<0时,不表示任何图形。
圆的定义的理解:
(1)定位条件:圆心;定形条件:半径。
(2)当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本的要素是圆心和半径.
圆的方程的理解:
(1)圆的标准方程中含有a,b,r三个独立的系数,因此,确定一个圆需三个独立的条件.其中圆心是圆的定位条件,半径是圆的定形条件.
(2)圆的标准方程的优点在于明确显示了圆心和半径.
(3)圆的一般方程形式的特点:
a.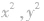 的系数相同且不等于零;
的系数相同且不等于零;
b.不含xy项.
(4)形如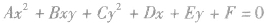 的方程表示圆的条件:
的方程表示圆的条件:
a.A=C≠0;
b.B=0;
c. 即
即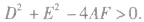
几种特殊位置的圆的方程:
| 条件 | 标准方程 | 一般方程 |
| 圆心在原点 |
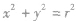 |
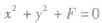 |
| 过原点 |
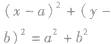 |
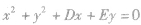 |
| 圆心在x轴上 |
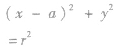 |
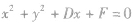 |
| 圆心在y轴上 |
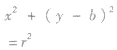 |
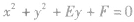 |
| 与x轴相切 |
 |
 |
| 与y轴相切 |
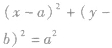 |
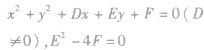 |
|
与x,y轴都相切 |
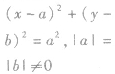 |
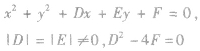 |
| 圆心在x轴上且过原点 |
 |
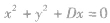 |
| 圆心在y轴上且过原点 |
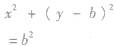 |
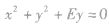 |
双曲线的离心率的定义:
(1)定义:双曲线的焦距与实轴长的比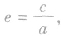 叫做双曲线的离心率.
叫做双曲线的离心率.
(2)e的范围:e>l.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.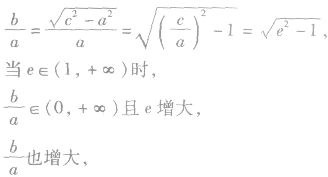
渐近线与实轴的夹角也增大。
双曲线的性质:
1、焦点在x轴上:顶点:(a,0),(-a,0);焦点:(c,0),(-c,0);
渐近线方程: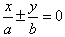 或
或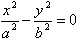 。
。
2、焦点在y轴上:顶点:(0,-a),(0,a);焦点:(0,c),(0,-c);
渐近线方程: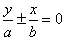 或
或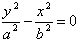 。
。
3、轴:x、y为对称轴,实轴长为2a,虚轴长为2b,焦距2c。
4、离心率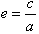 ;
;
5、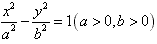 中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
双曲线的焦半径:
双曲线上的点 之间的线段长度称作焦半径,分别记作
之间的线段长度称作焦半径,分别记作

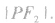
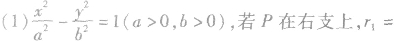
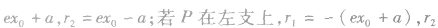
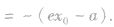
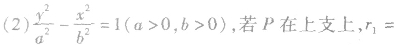
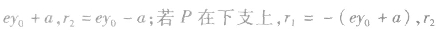

关于双曲线的几个重要结论:
(1)弦长公式(与椭圆弦长公式相同).
(2)焦点三角形:已知 的两个焦点,P为双曲线上一点(异于顶点),
的两个焦点,P为双曲线上一点(异于顶点),
 的面积为
的面积为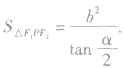
在解决与焦点三角形有关的问题时,应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用,还应注意灵活地运用平面几何、三角函数等知识来分析解决问题.
(3)基础三角形:如图所示,△AOB中,
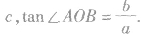
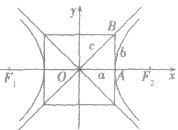 (4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长.
(4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长.
(5)自双曲线的焦点作渐近线的垂线,垂足必在相应的准线上,即过焦点所作的渐近线的垂线,渐近线及相应准线三线共点.
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切.
(7)双曲线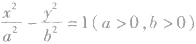 上一点P(x0,y0)处的切线方程是
上一点P(x0,y0)处的切线方程是
(8)双曲线划分平面区域:对于双曲线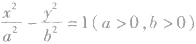 ,我们有:P(x0,y0)在双曲线内部(与焦点共区域)
,我们有:P(x0,y0)在双曲线内部(与焦点共区域)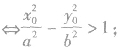 P(x0,y0)在双曲线外部(与焦点不其区域)
P(x0,y0)在双曲线外部(与焦点不其区域)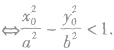
(2)焦点三角形:已知
 的两个焦点,P为双曲线上一点(异于顶点),
的两个焦点,P为双曲线上一点(异于顶点),
 的面积为
的面积为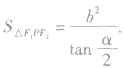
在解决与焦点三角形有关的问题时,应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用,还应注意灵活地运用平面几何、三角函数等知识来分析解决问题.
(3)基础三角形:如图所示,△AOB中,

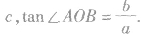

(5)自双曲线的焦点作渐近线的垂线,垂足必在相应的准线上,即过焦点所作的渐近线的垂线,渐近线及相应准线三线共点.
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切.
(7)双曲线
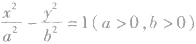 上一点P(x0,y0)处的切线方程是
上一点P(x0,y0)处的切线方程是
(8)双曲线划分平面区域:对于双曲线
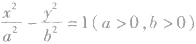 ,我们有:P(x0,y0)在双曲线内部(与焦点共区域)
,我们有:P(x0,y0)在双曲线内部(与焦点共区域)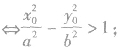 P(x0,y0)在双曲线外部(与焦点不其区域)
P(x0,y0)在双曲线外部(与焦点不其区域)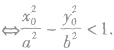
发现相似题
与“已知双曲线与圆交于A、B、C、D四点,若四边形ABCD是正方形,...”考查相似的试题有:
- 如图所示,己知为的边上一点,经过点,交于另一点,经过点,,交于另一点,与的另一交点为.(I)求证:四点共圆;(II)若切于,...
- 如图,切于点,割线经过圆心,弦于点。已知的半径为3,,则 。 。
- 已知两点M(-2,0),N(2,0),点P满足,则点P的轨迹方程为A.B.x2+y2=4C.y2-x2=8D.x2+y2=8
- 已知过A(0,1),B(1,2)的圆C的圆心在第一象限,且弧AB对的圆周角为π4.(1)求圆C的方程;(2)若D(2,-1),求∠ADB的...
- 若双曲线x236-y264=1上一点P到双曲线右焦点的距离是8,那么点P到双曲线左准线的距离是( )A.12B.125C.35D.377
- 已知双曲线与椭圆x225+y29=1的焦点相同,且它们的离心率之和等于145.(1)求双曲线的离心率的值;(2)求双曲线的标准方程.
- 已知双曲x29-y216=1,过其右焦点F的直线(斜率存在)交双曲线于P、Q两点,PQ的垂直平分线交x轴于点M,则|MF||PQ|的值为( )A...
- 双曲线的渐近线方程为A.x=±1B.y=±2C.y=±2xD.x=±2y
- 双曲线x2-16y2=16左右焦点分别为F1,F2,直线l过双曲线的左焦点F1交双曲线的左支与A,B,且|AB|=12,则△ABF2的周长为______.
- 已知方程x22-k+y2k-1=1的图象是双曲线,那么k∈( )A.(1,2)B.(-∞,1)∪(2,+∞)C.(-∞,1)D.(2,+∞)