本试题 “求过直线l1：x-2y+3=0与直线l2：2x+3y-8=0的交点，且到点P（0，4）的距离为1的直线l的方程．” 主要考查您对两条直线的交点坐标
点到直线的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 两条直线的交点坐标
- 点到直线的距离
两条直线的交点：
两直线：
，
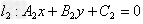，当它们相交时，方程组
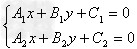有唯一的解，以这个解为坐标的点就是两直线的交点。
若方程组无解，两直线平行；若方程组有无数个解，则两直线重合。
两条直线的交点特别提醒：
①若方程组无解，则直线
平行；反之，亦成立；
②若方程组有无穷多解，则直线重合；反之，也成立；
③当有交点时，方程组的解就是交点坐标；
④相交的条件是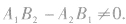
点到直线的距离公式：
1、若点P（x0，y0）在直线Ax+By+C=0（A，B不同时为0）上，则Ax0+By0+C=0。
2、若点P（x0，y0）不在直线Ax+By+C=0（A，B不同时为0）上，则Ax0+By0+C≠0，此时点P（x0，y0）直线Ax+By+C=0（A，B不同时为0）的距离d=
。
点到直线的距离公式的理解：
①点到直线的距离是直线上的点与直线外一点的连线的最短距离（这是从运动观点来看的）．
②若给出的直线方程不是一般式，则应先把方程化为一般式，再利用公式求距离．
③点到直线的距离公式适用于任何情况，其中点P在直线l上时，它到直线的距离为0．
④点到几种特殊直线的距离：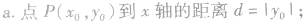
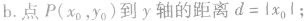
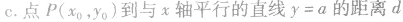
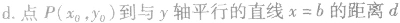
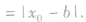
发现相似题
与“求过直线l1：x-2y+3=0与直线l2：2x+3y-8=0的交点，且到点P（0...”考查相似的试题有：
- 方程组的解集是（ ） A．（5，4） B．{5，-4} C．{（-5，4）} D．{（5，-4）}
- 如图，已知圆心坐标为的圆与轴及直线均相切，切点分别为、，另一圆与圆、轴及直线均相切，切点分别为、。（1）求圆和圆的方程...
- 已知双曲线x2-y2=1及点A（72，0）．（1）求点A到双曲线一条渐近线的距离；（2）已知点O为原点，点P在双曲线上，△POA为直角三...
- 将圆x2+y2+ 2x– 2y= 0按向量a= (1，–1)平移得到圆O，直线l和圆O相交于A、B两点，若在圆O上存在点C，使，且=a．（1）求的值；...
- 已知圆上有两点且满足，则直线的方程为____________________.
- 椭圆上的点到直线x+2y的最大距离是[ ]A．3B．C．D．
- 设、是关于x的方程的两个不相等的实数根，那么过两点，的直线与圆的位置关系是（ ）A．相离.B．相切.C．相交.D．随m的变化而变化
- 如图，已知两定点A（1，0），B（4，0），坐标xOy平面内的动点M满足，（Ⅰ）求动点M的轨迹C的方程并画出草图；（Ⅱ）是否存在过...
- 已知直线，若圆上恰好存在两个点P、Q，他们到直线的距离为1，则称该圆为“完美型”圆。则下列圆中是“完美型”圆的是（ ）A．B．C...
- 过原点且倾斜角为60°的直线被圆x2+y2－4y=0所截得的弦长为 .