本试题 “下列说法中,①等边三角形是等腰三角形;②三角形外角和大于这个三角形内角和;③四边形的内角最多可以有三个钝角;④多边形的对角线有7条,正确的个数有几个( ...” 主要考查您对多边形的内角和和外角和
多边形
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 多边形的内角和和外角和
- 多边形
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。
对角线:在多边形中,连接不相邻的两个顶点的线段叫做多边形的对角线。
外角:多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
如图示:
多边形的内角和:
n边形的内角和等于(n-2)·180°。(多边形内角和定理)
多边形的外角和:
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和。
多边形的外角和等于360°。(与边数无关) (多边形的外角和定理)
多边形外角和列举: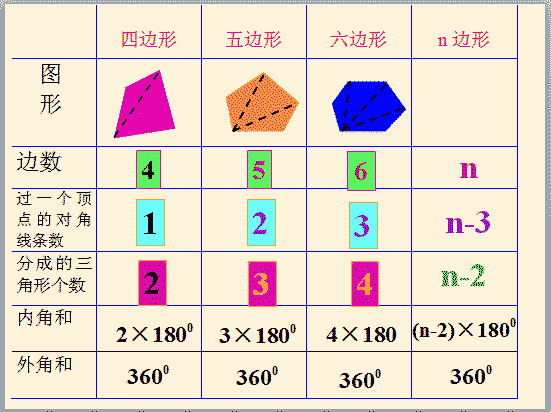
定义:
在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。如果一个图形有n条线段组成,那么这个多边形就叫做n边形,如四边形、五边形、六边形等。
多边形的内角:相邻两边组成的角叫做多边形的内角。
多边形的对角线:连结多边形不相邻的两个顶点的线段,叫做多边形的对角线。
多边形构成要素:
组成多边形的线段至少有3条,三角形是最简单的多边形。
组成多边形的每一条线段叫做多边形的边;
相邻的两条线段的公共端点叫做多边形的顶点;
多边形相邻两边所成的角叫做多边形的内角;
连接多边形的两个不相邻顶点的线段叫做多边形的对角线。
多边形内角的一边与另一边反向延长线所组成的角叫做多边形的外角。
多边形分类:
在多边形的每一个定点处取这个多边形的一个外角,它们的和叫做多边形的外角和。
多边形还可以分为正多边形和非正多边形。正多边形各边相等且各内角相等。
多边形也可以分为凸多边形及凹多边形,凸多边形又可称为平面多边形,凹多边形又称空间多边形
(此定理只适用于凸多边形,即平面多边形,空间多边形不适用)广义的多边形也包括五角星等图形。
在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。如果一个图形有n条线段组成,那么这个多边形就叫做n边形,如四边形、五边形、六边形等。
多边形的内角:相邻两边组成的角叫做多边形的内角。
多边形的对角线:连结多边形不相邻的两个顶点的线段,叫做多边形的对角线。
多边形构成要素:
组成多边形的线段至少有3条,三角形是最简单的多边形。
组成多边形的每一条线段叫做多边形的边;
相邻的两条线段的公共端点叫做多边形的顶点;
多边形相邻两边所成的角叫做多边形的内角;
连接多边形的两个不相邻顶点的线段叫做多边形的对角线。
多边形内角的一边与另一边反向延长线所组成的角叫做多边形的外角。
多边形分类:
在多边形的每一个定点处取这个多边形的一个外角,它们的和叫做多边形的外角和。
多边形还可以分为正多边形和非正多边形。正多边形各边相等且各内角相等。
多边形也可以分为凸多边形及凹多边形,凸多边形又可称为平面多边形,凹多边形又称空间多边形
(此定理只适用于凸多边形,即平面多边形,空间多边形不适用)广义的多边形也包括五角星等图形。
多边形定理:
1、内角和定理:
n边形的内角和等于(n-2)x180°
可逆用:
·n边形的边=(内角和÷180°)+2
·过n边形一个顶点有(n-3)条对角线
·因为每个顶点和它自己及相邻的两个顶点都不能做对角线,所以n边形的每个顶点只能和n-3个其他的顶点之间做对角线,又因为每一条对角线都要连结两个顶点,所以要除以2。
n边形共有n×(n-3)÷2个对角线
· n边形过一个顶点引出所有对角线后,把多边形分成n-2个三角形
推论:
·任意凸形多边形的外角和都等于360°。
·多边形对角线的计算公式:n边形的对角线条数等于1/2·n(n-3)
·在平面内,各边相等,各内角也都相等的多边形叫做正多边形。【两个条件必须同时满足
反例:矩形(各内角相等,各边不一定相等);菱形(各边相等,各内角不一定相等)】
2、外角和定理:
n边形外角和等于n·180°-(n-2)·180°=360°
多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°
发现相似题
与“下列说法中,①等边三角形是等腰三角形;②三角形外角和大于这...”考查相似的试题有:
- 点M、N分别是正八边形相邻的边AB、BC上的点,且AM=BN,点O是正八边形的中心,则∠MON=( )度。
- 多边形的每一个内角都是150°,则这个多边形是______边形,从这个多边形的一个顶点出发有______条对角线.
- 一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是[ ]A.5B.6C.7D.8
- 一个边形的内角和等于1080°,则这个多边形的对角线有( )条。
- 清晨,小强沿着一个五边形广场周围的小路,按逆时针方向跑步.(1)小强每从一条街道转到下一条街道时,身体转过的角是哪些角...
- 一个多边形的所有内角和与其中一个外角的度数和为1370°,则该多边形的边数为( )A.7B.8C.9D.10
- 若正多边形的一个外角为30°,则这个多边形为正______边形.
- 一个多边形的每个外角都为30°,那么这个多边形的边数n=( )。
- 正五边形的每一个内角都等于______°.
- 多边形的对角线的总数d与边数n的关系式为______.