本试题 “(1)求函数y=log0.5(4x3-3x)+(x-1)0的定义域(2)设a>0且a≠1,解关于x的不等式a2x2-3x+2>a2x2+2x-3.” 主要考查您对函数的定义域、值域
指数函数的图象与性质
一元高次(二次以上)不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
- 指数函数的图象与性质
- 一元高次(二次以上)不等式
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则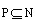 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如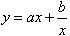 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
指数函数y=ax(a>0,且a≠1)的图象和性质:
| 0<a<1 | a>1 | ||
| 图像 | 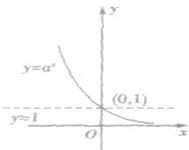 |
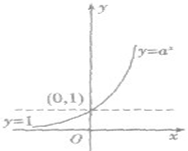 | |
| 图像 | 定义域 | R | |
| 值域 | (0,+∞) | ||
| 恒过定点 | 图像恒过定点(0,1),即当x等于0时,y=1 | ||
| 单调性 | 在(-∞,+∞)上是减函数 | 在(-∞,+∞)上是增函数 | |
| 函数值的变化规律 | 当x<0时,y>1 | 当x<0时,0<y<1 | |
| 当x=0时,y=1 | 当x=0时,y=1 | ||
| 当x>0时,0<y<1 | 当x>0时,y>1 | ||
底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.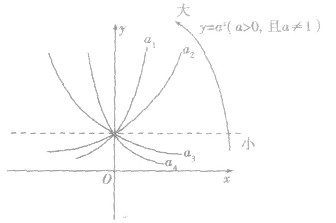
③当a>0,且a≠l时,函数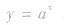 与函数y=
与函数y=![]() 的图象关于y轴对称。
的图象关于y轴对称。
利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值,
指数函数图象的应用:
函数的图象是直观地表示函数的一种方法.函数的很多性质,可以从图象上一览无余.数形结合就是几何与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变可得出一般函数的图象.利用指数函数的图象,可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题.
元高次不等式的概念:
含有一个未知数且未知数的最高次数不小于3的不等式叫做一元高次不等式
一元高次不等式的解法:
①解一元高次不等式时,通常需进行因式分解,化为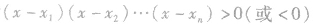 的形式,然后应用区间法化为不等式组或用数轴标根法求解集.
的形式,然后应用区间法化为不等式组或用数轴标根法求解集.
②用数轴标根法求解一元高次不等式的步骤如下:
a.化简:将原不等式化为和它同解的基本型不等式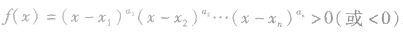 .其中
.其中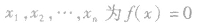 的n个根,它们两两不等,通常情况下,常以
的n个根,它们两两不等,通常情况下,常以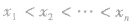 的形式出现,
的形式出现,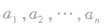 为相同因式的幂指数,它们均为自然数,可以相等;
为相同因式的幂指数,它们均为自然数,可以相等;
b.标根:将 标在数轴上,将数轴分成(n+1)个区间;
标在数轴上,将数轴分成(n+1)个区间;
c.求解:若 ,则从最右边区间的右上方开始画一条连续的曲线,依次穿过每一个零点(
,则从最右边区间的右上方开始画一条连续的曲线,依次穿过每一个零点(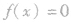 的根对应的数轴上的点),穿过最左边的零点后,曲线不再改变方向,向左下或左上的方向无限伸展.这样,不等式
的根对应的数轴上的点),穿过最左边的零点后,曲线不再改变方向,向左下或左上的方向无限伸展.这样,不等式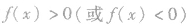 的解集就直观、清楚地表示在图上,这种方法叫穿针引线法(或数轴标根法);当
的解集就直观、清楚地表示在图上,这种方法叫穿针引线法(或数轴标根法);当 不全为l,即f(x)分解因式出现多重因式(即方程f(x)=0出现重根)时,对于奇次重因式对应的根,仍穿轴而过;对于偶次重因式对应的根,则应使曲线与轴相切.简言之,函数f(x)中有重因式时,曲线与轴的关系是"奇穿偶切".
不全为l,即f(x)分解因式出现多重因式(即方程f(x)=0出现重根)时,对于奇次重因式对应的根,仍穿轴而过;对于偶次重因式对应的根,则应使曲线与轴相切.简言之,函数f(x)中有重因式时,曲线与轴的关系是"奇穿偶切".
与“(1)求函数y=log0.5(4x3-3x)+(x-1)0的定义域(2)设a>0且...”考查相似的试题有:
- 函数(x∈R)的值域是( )。
- 已知函数的值域为,则的取值范围是 .
- 设函数f(x)=(>0, 且1),[m]表示不超过实数m的最大整数,则函数[f(x)]+[f]的值域是( )A.{-,}B.{-1, 0}C.{-1, 1}D.{0}
- 函数f(x)=的定义域是( )。
- 函数的定义域为 。
- 将指数函数f(x)的图象向右平移一个单位,得到如图的g(x)的图象,则f(x)=[ ]A.B.C.2xD.3x
- 设集合A={x|x2-4<0},B={x|4x+3>1}.( I)求集合CRA∩B;( II)若不等式2x2+ax+b<0的解集为B,求a,b的值.
- 已知函数f(x)=ax+1,(0<x<a).3-xa+1,(a≤x<1)满足f(a2)=2827.(Ⅰ)求常数a的值;(Ⅱ)解不等式f(x)>1+327.
- 不等式x-1x+4>0的解集为______.
- 对于任意实数x,符号[x]表示x的整数部分,即[x]是不超过x的最大整数”.在实数轴R(箭头向右)上[x]是在点x左侧的第一个整数点...