本试题 “已知二次函数f(x)=ax2+bx+c及一次函数g(x)=-bx。(1)若a>b>c,a+b+c=0,设f(x)与g(x)两图像交于A,B两点,当线段AB在x轴上射影为A1B1时,试求|A1B...” 主要考查您对不等式的定义及性质
基本不等式及其应用
一元二次方程及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 不等式的定义及性质
- 基本不等式及其应用
- 一元二次方程及其应用
不等式的定义:
一般地,用不等号表示不相等关系的式子叫做不等式,常见的不等号有“<”“>”“ ≤”“≥”及“≠”。
严格不等式的定义:
用“>"“<”连接的不等式叫做严格不等式。
非严格不等式的定义:
用“≤”和“≥”连接的不等式叫做非严格不等式.
特别提醒:a=b,a>b中,只要有一个成立,就有a≥b.
不等式的性质:
(1)如果a>b,那么b<a;如果b<a,那么a>b,即a>b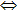 b<a;
b<a;
(2)如果a>b,b>c,那么a>c,即a>b,b>c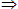 a>c;
a>c;
(3)如果a>b,那么a+c>b+c;
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac<bc;
(5)如果a>b,c>d,那么a+c>b+d;
(6)如果a>b>0,c>d>0,那么ac>bd;
(7)如果a>b>0,那么an>bn(n∈N,n≥2);
(8)如果a>b>0,那么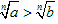 (n∈N,n≥2)。
(n∈N,n≥2)。
不等关系与不等式的区别:
不等关系强调的是量与量之间的关系,可以用符号“<…>…≤”“≥”来表示,也可以用语言表述;
而不等式则是用来表示不等关系的式子,可用“a>b”‘a<b”“a≥b a≤b”等式子来表示,不等关系是通过不等式来体现的.
不等式的分类:
①按成立的条件分:a.绝对不等式:不等式中的字母取任意实数值都恒成立的不等式叫做绝对不等式;b.条件不等式:不等式中的字母取某些允许值才能成立的不等式叫做条件不等式;c.矛盾不等式:不等式中的字母不论取何实数值都不能成立的不等式叫做矛盾不等式;
②按不等号开口方向分:a.同向不等式:不等号方向相同的两个不等式;b.异向不等式:不等号方向相反的两个不等式.
基本不等式:
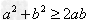 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①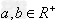 ,
,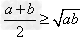 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②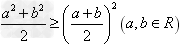 ;③
;③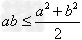 ;④
;④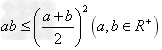 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有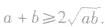
(2)基本不等式又称为均值定理、均值不等式等,其中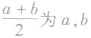 的算术平均数,
的算术平均数,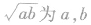 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即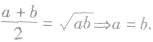
对于两个正数x,y,若已知xy,x+y,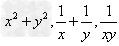 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2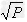 ,
,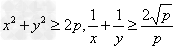 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值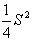 ,
,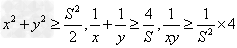 ;
;
(3)已知x2+y2=p,则x+y有最大值为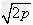 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式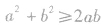 的形式可以是
的形式可以是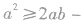
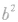 ,也可以是
,也可以是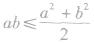 ,还可以是
,还可以是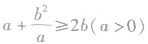 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

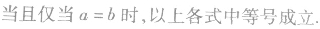
一元二次方程的定义:
含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:
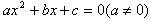 。
。
一元二次方程的应用:
建立一元二次方程模型进行求解,把得到的答案带回实际问题中检验是否合理,来解决实际问题,如打折、营销、增长率问题等。
一元二次方程的根与系数的关系:
如果方程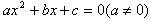 的两个实数根是
的两个实数根是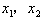 ,那么
,那么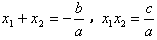 。
。
与“已知二次函数f(x)=ax2+bx+c及一次函数g(x)=-bx。(1)若a...”考查相似的试题有:
- 试比较x2+y2与xy+x+y-1的大小.
- 若a>b>c,则一定成立的不等式是( )A.a|c|>b|c|B.ab>acC.a-|c|>b-|c|D.1a<1b<1c
- 若关于的不等式恒成立,则的取值范围是( )A.B.C.D.
- 若b<a<0列结论不正确的是( )A.a2<b2B.ab<b2C.(12)b<(12)aD.ab+ba>2
- 用一张钢板制作一个容积为4 m3的无盖长方体水箱.可用的长方形钢板有四种不同的规格(长×宽的尺寸如各选项所示,单位均为m)...
- 设实数m,n,x,y满足m2+n2=3,x2+y2=4,则mx+ny的最大值为______.
- 对于使f(x)≤M恒成立的所有常数M中,我们把M的最小值叫做f(x)的上确界,若a>0,b>0,且a+b=1,则的上确界为( )。
- 设,则的最小值是( )A.1B.2C.3D.4
- 已知,则的最小值为 .
- 已知不等式xy≤ax2+2y2对于x∈[1,2],y∈[2,3]恒成立,则实数a的取值范围是( )。