本试题 “为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个50m2的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和...” 主要考查您对频率分布表、频率分布直方图、频率分布折线图、茎叶图
独立性检验的基本思想及其初步应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 频率分布表、频率分布直方图、频率分布折线图、茎叶图
- 独立性检验的基本思想及其初步应用
频率分布:
样本中所有数据(或者数据组)的频率和样本容量的比就是该数据的频率,所有数据(或者数据组)的频率的分布变化规律叫做频率分布,可以用频率分布表,频率分布折线图,茎叶图,频率分布直方图来表示.
频率分布折线图:
如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图。
频数分布表:
反映总体频率分布的表格。
一般地,编制频率分布表的步骤如下:(1)求全距,决定组数和组距;(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表。
茎叶图:
(1)茎是指中间的一列数,叶是从茎的旁边生长出来的数。
(2)制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出;
(3)茎叶图的性质: ①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
茎叶图的性质:
①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
作频率分布直方图的步骤:
①求极差,即一组数据中最大值和最小值的差。
②决定组距与组数.将数据分组时,组数应力求合适,以使数据的分布规律能较清楚的呈现出来。这时应注意:a.一般样本容量越大,所分组数越多;b.为方便起见,组距的选择应力求“取整”;c.当样本容量不超过100时,按照数据的多少,通常分成5组~l2组.
③将数据分组.
④计算各小组的频率(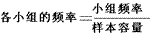 ),作频率分布表。
),作频率分布表。
⑤画频率分布直方图。
与“为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200...”考查相似的试题有:
- 已知一组数据x1,x2,x3,…,xn的平均数是,方差是,那么另一组数据2x1– 1,2x2– 1,2x3– 1,…,2xn– 1的平均数是 ,方差是 .
- 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范...
- 某中学的高二(1)班男同学有名,女同学有名,老师按照分层抽样的方法组建了一个人的课外兴趣小组.(Ⅰ)求某同学被抽到的概率...
- 为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,...
- 某市2010年4月1日-4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物): 61,76,70,56,81,91,92,91,75...
- 在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到...
- 某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员...
- 甲、乙两个学习小组各有10名同学,他们在一次数学测验中的成绩可用下面的茎叶图表示,则在这次测验中成绩较好的是( )组。
- 为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个50m2的小块,并在100个小块上施用新化肥,留下100个条件大体相...
- 为考察某种甲型H1N1疫苗的效果,进行动物试验,得到如丢失数据的列联表:设从没服疫苗的动物中任取两只,未感染数为ξ;从服用...