本试题 “给出下列四个命题:①若△ABC三边为a,b,c,面积为S,内切圆的半径,则由类比推理知四面体ABCD的内切球半径(其中,V为四面体的体积,为四个面的面积);②若回...” 主要考查您对函数的奇偶性、周期性
圆与圆的位置关系
线性回归分析
合情推理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的奇偶性、周期性
- 圆与圆的位置关系
- 线性回归分析
- 合情推理
函数的奇偶性定义:
偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性:
(1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。
奇函数与偶函数性质:
(1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。
注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
2、函数的周期性 令a , b 均不为零,若:
(1)函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
(2)函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
(3)函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
(4)函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|2a|
==> 函数最小正周期 T=|2a|
(5)函数y = f(x) 存在 f(x + a) = 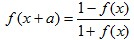 ==> 函数最小正周期 T=|4a|
==> 函数最小正周期 T=|4a|
圆与圆的位置关系:
圆与圆有五种位置关系:相交、外离、外切、内切和内含。
圆与圆的位置关系的判断方法:
(1)利用圆心距和两圆半径比较大小(几何法)已知两圆
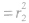 的圆心距为d
的圆心距为d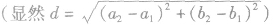 ,则位置关系表示如下:
,则位置关系表示如下: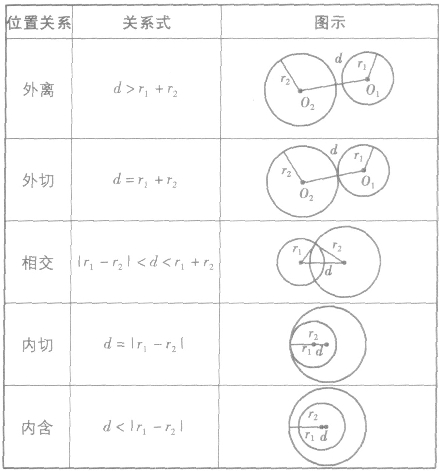
(2)利用两圆的交点进行判断(代数法)
设由两圆的方程组成的方程组为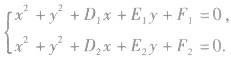
由此方程组得:有两组不同的实数解则两圆相交;有两组相同的实数解则两圆相切;无实数解则两圆相离.
两圆公切线条数的确定:
两圆的公切线的条数是由两圆的位置关系确定的,设两圆的圆心距为d,两圆的半径分别为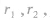
则当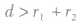 时,两圆外离,此时有四条公切线;
时,两圆外离,此时有四条公切线;
当 时,两圆外切,连心线过切点,此时有三条公切线,有外公切线两条,内公切线一条;
时,两圆外切,连心线过切点,此时有三条公切线,有外公切线两条,内公切线一条;
当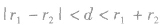 时,两圆相交,连心线垂直平分公共弦,有两条外公切线;
时,两圆相交,连心线垂直平分公共弦,有两条外公切线;
当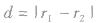 时,两圆内切,连心线过切点,此时只有一条公切线;
时,两圆内切,连心线过切点,此时只有一条公切线;
当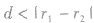 时,两圆内含,此时没有公切线。
时,两圆内含,此时没有公切线。
回归直线:
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线;
最小二乘法:
使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法。
回归直线方程:
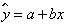 ,
,
其中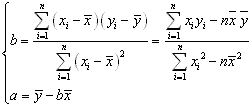 。
。
回归分析是处理变量相关关系的一种常用数学方法,其步骤为:
(1)确定特定量之间是否有相关关系,如果有,那么就找出他们之间贴近的数学表达式;
(2)根据一组观察值,预测变量的取值及判断变量取值的变化趋势;
(3)求出回归直线方程。
归纳推理的定义:
根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理,叫做归纳推理(简称归纳)。归纳是从特殊到一般的过程,它属于合情推理;
类比推理的定义:
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,叫做类比推理(简称类比)。类比推理是由特殊到特殊的推理。
类比推理的一般步骤:
(1)找出两类事物之间的相似性或一致性;
(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想);
(3)一般地,事物之间的各个性质之间并不是孤立存在的,而是相互制约的。如果两个事物在某些性质上相同或类似,那么它们在另一些性质上也可能相同或类似,类比的结论可能是真的;
(4)在一般情况下,如果类比的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的命题就越可靠。
归纳推理的一般步骤:
①通过观察个别情况发现某些相同性质;
②从已知的相同性质中推出一个明确表达的一般性命题(猜想).
归纳推理和类比推理的特点:
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,统称为合情推理。
归纳推理的应用方法:
归纳推理是由部分到整体、由个别到一般的推理,要注意探求的对象的本质属性与因果关系.与数列有关的问题,要联想等差、等比数列,把握住数的变化规律.
类比推理的应用方法:
合情推理的正确与否来源于平时知识的积累,如平面到空间、长度到面积、面积到体积、平面中的点与空间中的直线、平面中的直线与空间巾的平面.
与“给出下列四个命题:①若△ABC三边为a,b,c,面积为S,内切圆的...”考查相似的试题有:
- 已知函数f(x)的定义域为D:(-∞,0)∪(0,+∞),且满足对于任意x,y∈D,有f(xy)=f(x)+f(y).(I)求f(1),f(-1)...
- 定义在R上的函数f(x)满足f(x)=则f(2014)=________.
- 已知y=f(x)是定义在R上的奇函数,且y=f(x+π2)为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一...
- 设f(x)是R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=A.3B.1C.-1D.-3
- 已知函数f(x)=x2+2x+alnx.(Ⅰ)若a=-4,求函数f(x)的极值;(Ⅱ)当t≥1时,不等式f(2t-1)≥2f(t)-3恒成立,求实数a的...
- 定义在[-2,2]上的偶函数f(x)在区间[0,2]上是减函数,且f(1-m)<f(m),则m∈( )
- 若f(x)是偶函数,其定义域为(-∞,+∞),且在[0,+∞)上是减函数,则与的大小关系是[ ]A、>B、<C、≥D、≤
- 若存在实常数k和b,使函数f(x)和g(x)对其定义域上的任意实数x恒有:f(x)≥kx+b和g(x)≤kx+b,则称直线l:y=kx+b为f(x...
- 已知:偶函数f(x)在(0,+∞)上是增函数,判断f(x)在(-∞,0)上的单调性,并证明你的结论.
- 已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )A.=1.23x+4B.=1.23x+5C.=1.23x+0.08D.=0.0...