本试题 “设函数f(x)=﹣x﹣2,x∈[﹣5,5].若从区间[﹣5,5]内随机选取一个实数,则所选取的实数满足f()≤0的概率为[ ]A.0.5B.0.4C.0.3D.0.2” 主要考查您对几何概型的定义及计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 几何概型的定义及计算
几何概型的概念:
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)称比例,则称这样的概率模型为几何概率模型,简称为几何概型。
几何概型的概率:
一般地,在几何区域D中随机地取一点,记事件"该点落在其内部一个区域d内"为事件A,则事件A发生的概率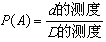 。
。
说明:(1)D的测度不为0;
(2)其中"测度"的意义依D确定,当D分别是线段,平面图形,立体图形时,相应的"测度"分别是长度,面积和体积;
(3)区域为"开区域";
(4)区域D内随机取点是指:该点落在区域内任何一处都是等可能的,落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关.
几何概型的基本特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等.
发现相似题
与“设函数f(x)=﹣x﹣2,x∈[﹣5,5].若从区间[﹣5,5]内随机选...”考查相似的试题有:
- 记函数的图象与轴围成的区域为M,满足的区域为N,若向区域M上随机投一点P,则点P落入区域N的概率为______
- 为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部...
- 如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是[ ]A...
- 如果每个事件发生的概率只与构成事件区域的______,______成比例,则称这样的概率模型为几何概率模型,简称为几何概型.
- 设函数.若从区间内随机选取一个实数,则所选取的实数满足的概率为( )A.B.C.D.
- 在边长为1的正方形ABCD中任取一点P,则的面积大于的概率是( )A.B.C.D.
- 已知函数,在区间上随机取一个数,则使得≥0的概率为 .
- 设函数f(x)=﹣x﹣2,x∈[﹣5,5].若从区间[﹣5,5]内随机选取一个实数,则所选取的实数满足f()≤0的概率为[ ]A.0.5B.0.4...
- (1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒.当你到达路口时,求不是红灯的概率.(2)已知关于x...
- 如图所示,甲、乙两人玩转盘游戏,规定当指针指向阴影所示区域时甲胜,否则乙胜,则甲获胜的概率是( )。