本试题 “(10分)如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.(1)求证:MN//平面PAD(2)求证:MN⊥CD(3)若∠PDA=45°,求证:MN⊥平面PCD.” 主要考查您对点到直线、平面的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 点到直线、平面的距离
点到直线的距离:
由点向直线引垂线,这一点到垂足之间的距离。
点到平面的距离:
由点向平面引垂线,这点到垂足之间的距离,就叫做点到平面的距离。
求点面距离常用的方法:
(1)直接利用定义
①找到(或作出)表示距离的线段;
②抓住线段(所求距离)所在三角形解之.
(2)利用两平面互相垂直的性质如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离.
(3)体积法其步骤是:①在平面内选取适当三点和已知点构成三棱锥;②求出此三棱锥的体积V和所取三点构成三角形的面积S;③由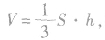 求出
求出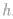 .这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
.这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
(4)转化法:将点到平面的距离转化为直线与平面的距离来求.
(5)向量法:

发现相似题
与“(10分)如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点...”考查相似的试题有:
- 在正三棱锥中,分别是的中点,有下列三个论断:①;②//平面;③平面,其中正确论断的个数为 ( )A.3个 B.2个C.1个D.0个
- 如图,四边形PCBM是直角梯形,,∥,.又,,直线AM与直线PC所成的角为.(1)求证:;(2)求二面角的余弦值.
- (本小题满分14分)已知棱长为1的正方体ABCD-A1B1C1D1中,P在对角线A1C1上,记二面角P-AB-C为α,二面角P-BC-A为β。(1)当A1P:...
- 空间中一个角∠A的两边和另一个角∠B的两边分别平行,若∠A=,则∠B= ___________;
- 平行四边形的一个顶点A在平面α内,其余顶点在α的同侧,已知其中有两个顶点到α的距离分别为1和2,那么剩下的一个顶点到平面α的...
- 将正方形沿对角线折成直二面角,有如下四个结论:①⊥;②△是等边三角形;③与平面所成的角为60°;④与所成的角为60°.其中错误的结论...
- (本小题满分13分)已知,在水平平面上有一长方体绕旋转得到如图所示的几何体.(Ⅰ)证明:平面平面;(Ⅱ)当时,直线与平面所...
- (本小题满分12分)如图,菱形ABCD与矩形BDEF所在平面互相垂直,.(1)求证:FC∥平面AED;(2)若,当二面角为直二面角时,...
- 已知正四棱柱ABCD-A1B1C1D1,AB=1,AA1=2,点E为CC1中点,点F为BD1中点。(1)证明EF为BD1与CC1的公垂线;(2)求点D1到面BDE...
- 已知、是两条不同的直线,、是两个不同的平面,则下列命题中正确的是A.若,且,则B.若,且,则C.若,且,则D.若,且,则