返回

初中数学

首页
首页 初中数学知识 一元一次不等式组的解法 二次函数与一元二次方程 试题正文
  • 解答题
    当关于x的不等式组
    x＞a+2
    x＜3a-2
    无解时，请判断函数y=（3-a）x2-x+
    1
    4
    的图象与x轴交点的情况，并说明理由．
    本题信息：数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “当关于x的不等式组x＞a+2x＜3a-2无解时，请判断函数y=（3-a）x2-x+14的图象与x轴交点的情况，并说明理由．” 主要考查您对

一元一次不等式组的解法

二次函数与一元二次方程

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 一元一次不等式组的解法
  • 二次函数与一元二次方程

一元一次不等式组解集：
一元一次不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集。
注：当任何数x都不能使各个不等式同时成立，我们就说这个一元一次不等式组无解或其解集为空集。
例如：
不等式x-5≤-1的解集为x≤4；
不等式x﹥0的解集是所有非零实数。
解法：求不等式组的解集的过程，叫做解不等式组。


求几个一元一次不等式的解集的公共部分，通常是利用数轴来确定的，公共部分是指数轴上被两条不等式解集的区域都覆盖的部分；
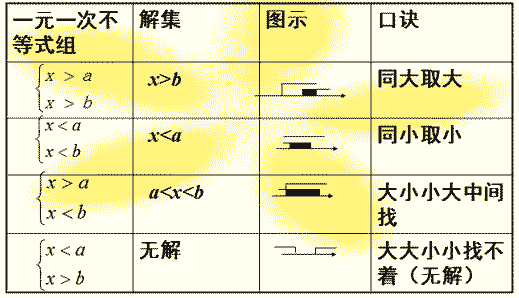
一般由两个一元一次不等式组成的不等式组由四种基本类型确定，它们的解集、数轴表示如下表：（设a<b）

一元一次不等式组的解答步骤：
（1）分别求出不等式组中各个不等式的解集；
（2）将这些不等式的解集在同一个数轴上表示出来，找出它们的的公共部分；
（3）根据找出的公共部分写出不等式组的解集，若没有公共部分，说明不等式组无解。

解法诀窍：
同大取大 ；
例如：
X>-1
X>2
不等式组的解集是X>2

同小取小；
例如：
X<-4
X<-6
不等式组的解集是X<-6

大小小大中间找；
例如，
x<2,x>1,不等式组的解集是1<x<2

大大小小不用找
例如，
x<2,x>3，不等式组无解


一元一次不等式组的整数解：
一元一次不等式组的整数解是指在不等式组中各个不等式的解集中满足整数条件的解的公共部分。
求一元一次不等式组的整数解的一般步骤：先求出不等式组的解集，再从解集中找出所有整数解，其中要注意整数解的取值范围不要搞错。
例如



所以原不等式的整数解为1，2。


二次函数与一元二次方程的关系：
函数y=ax2+bx+c（a≠0），当y=0时，得到一元二次方程ax2+bx+c=0（a≠0）。
那么一元二次方程的解就是二次函数图像与x轴焦点的横坐标，因此，二次函数图像与x轴的交点情况决定一元二次方程根的情况。
1、从形式上看：
二次函数：y=ax2＋bx＋c  (a≠0)
一元二次方程：ax2＋bx＋c=0  (a≠0)
2、从内容上看：
二次函数表示的是一对(x，y)之间的关系，它有无数对解；一元二次方程表示的是未知数x的值，最多只有2个值
3、相互关系：
二次函数与x轴交点的横坐标就是相应的一元二次方程的根。
如：y=x2－4x＋3与x轴的交点是(1，0)、(3，0)，则一元二次方程x2－4x＋3=0的根是x=1或x=3

二次函数交点与二次方程根的关系：
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明：
1、若△＞0，则一元二次方程ax2+bx+c=0有两个不等的实数根，则抛物线y=ax2+bx+c与x轴有两个交点---相交；
2、若△=0，则一元二次方程ax2+bx+c=0有两个相等的实数根，则抛物线y=ax2+bx+c与x轴有唯一公共点---相切（顶点）；
3、若△＜0，则一元二次方程ax2+bx+c=0没有实数根，则抛物线y=ax2+bx+c与x轴没有公共点--相离。
若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A（x1，0），B（x2，0），则x1+x2=-，x1x2=。


点拨：
①解一元二次方程实质上就是求当二次函数值为0时的自变量x的取值，反映在图像上就是求抛物线与x轴交点的横坐标。
②若一元二次方程ax2+bx+c=0（a≠0）的两根为x1,x2(x1<x2),则抛物线y=ax2+bx+c与x轴的交点为（x1,0）,(x2,0),对称轴为x=x1+x2/2。
③若a>0,当x<x1,或x>x2时，y>0;当x1<x<x2时，y<0。
若a< 0,当x1<x<x2时，y>0;当x<x1或x>x2时，y<0。
④如果抛物线y=ax2+bx+c与x轴交于M（x1，0），N(x2，0)，则MN=√b2-4ac/|a|。


发现相似题
与“当关于x的不等式组x＞a+2x＜3a-2无解时，请判断函数y=（3-a）...”考查相似的试题有：