本试题 “直线l的方向向量为=(4 , 3)且过抛物线x2=4y的焦点,则直线l与抛物线围成的封闭图形面积为( ) A. B. C. D.” 主要考查您对定积分的简单应用
直线的方向向量
抛物线的性质(顶点、范围、对称性、离心率)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 定积分的简单应用
- 直线的方向向量
- 抛物线的性质(顶点、范围、对称性、离心率)
定积分的简单应用:
1、求几何图形的面积:在直角坐标系中,由曲线f(x),直线x=a,x=b(a<b)和x轴围成的曲边梯形的面积,当对应的曲边梯形位于x轴上方时,定积分的取值为正值;当对应的曲边梯形位于x轴下方时,定积分的取值为负值;当位于x轴上方的曲边梯形面积等于位于x轴下方的曲线梯形面积时,定积分的值为0.
2、变速运动问题:如果变速运动的物体的速度v关于时间t的函数是v=v(t)(v(t)≥0),那么物体从时刻t=a到t=b所经过的路程为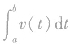 如果变速运动的物体的速度v关于时间t的函数是v=v(t)
如果变速运动的物体的速度v关于时间t的函数是v=v(t)
(v(t)≤0),那么物体从时刻t=a到t=b所经过的路程为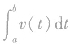 。
。
求定积分的方法:
方法1:用定义求定积分的一般步骤:
(1)分割:n等分区间[a,b];
(2)近似代替:取点ξi∈[xi-1,xi];
(3)求和:
(4)取极限:
方法2:用所求定积分表示的几何意义求积分
当定积分表示的面积容易求时,则利用定积分的几何意义求积分.
点P的位置向量:
在空间中,我们取一定点O作为基点,那么空间中任意一点P的位置就可以用向量OP老表示,我们把向量OP成为点P的位置向量。
直线的方向向量的定义:
(1)空间中任意一条直线l的位置可由l上一个定点A以及一个定方向确定。直线l上的向量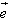 以及与
以及与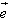 共线的向量叫做直线l的方向向量。
共线的向量叫做直线l的方向向量。
对于直线l上的任意一点P,存在实数t使得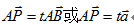 (如图所示)。
(如图所示)。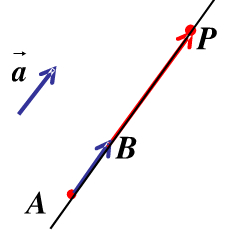
(2)由于垂直于同一平面的直线是互相平行的,所以,可以用垂直于平面的直线的方向向量来刻画平面的“方向”。
抛物线的性质(见下表):

抛物线的焦点弦的性质:

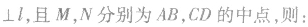

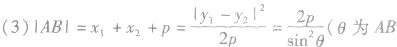

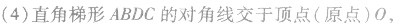


关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部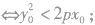 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部
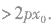
(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F, 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。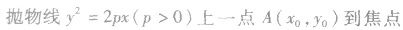
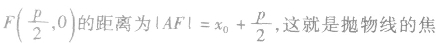
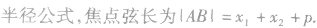
与“直线l的方向向量为=(4 , 3)且过抛物线x2=4y的焦点,则直线l...”考查相似的试题有:
- 变速运动的物体的速度为v(t)=1-t2m/s(其中t为时间,单位:s),则它在前2s内所走过的路程为( ) A.- B. C.-2 D.2
- (本小题满分12分)已知是边长为2的等边三角形,平面,,是上一动点.(1)若是的中点,求直线与平面所成的角的正弦值;(2)...
- 若抛物线y2=2px(p>0)的焦点与双曲线x2-y2=2的右焦点重合,则p的值为______.
- 若抛物线y2=2px的焦点与椭圆的右焦点重合,则实数p的值是( )
- 抛物线y2=-8x的焦点坐标为( )。
- 抛物线y2=4x图象上与其准线的距离为5的点的坐标为( )A.(4,±4)B.(3,±23)C.(2,±22)D.(1,±2)
- 设抛物线y2=4x的焦点弦被焦点分为长是m和n的两部分,则m与n的关系是______.
- 已知A,B是抛物线x2=4y上两个动点,且直线AO与直线BO的倾斜角之和为π4,试证明直线AB过定点.
- 抛物线y2=4x的准线方程是______,焦点坐标是______.
- 设抛物线y2=4x上一点P到y轴的距离是2,则点P到该抛物线焦点的距离是( )A.1B.2C.3D.4