本试题 “已知向量,且,则tanx=[ ]A.0B.1C.2D.” 主要考查您对同角三角函数的基本关系式
向量共线的充要条件及坐标表示
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 同角三角函数的基本关系式
- 向量共线的充要条件及坐标表示
同角三角函数的关系式:
(1)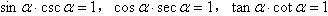 ;
;
(2)商数关系: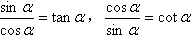 ;
;
(3)平方关系: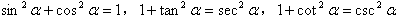 。
。
同角三角函数的基本关系的应用:
已知一个角的一种三角函数值,根据角的终边的位置利用同角三角函数的基本关系,可以求出这个角的其他三角函数值.
同角三角函数的基本关系的理解:
(1)在公式中,要求是同一个角,如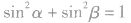 不一定成立.
不一定成立.
(2)上面的关系式都是对使它的两边具有意义的那些角而言的,如:基本三角关系式 。对一切α∈R成立;
。对一切α∈R成立;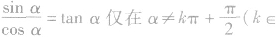 Z)时成立.
Z)时成立.
(3)同角三角函数的基本关系的应用极为为广泛,它们还有如下等价形式: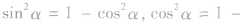

(4)在应用平方关系时,常用到平方根、算术平方根和绝对值的概念,应注意“±”的选取.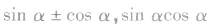 间的基本变形 三者通过
间的基本变形 三者通过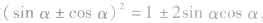 ,可知一求二,有关
,可知一求二,有关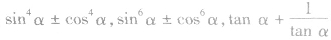 等化简都与此基本变形有广泛的联系,要熟练掌握。
等化简都与此基本变形有广泛的联系,要熟练掌握。
向量共线的充要条件:
向量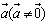 与
与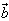 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得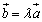 。
。
向量共线的几何表示:
设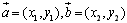 ,其中
,其中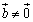 ,当且仅当
,当且仅当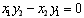 时,向量
时,向量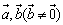 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
发现相似题
与“已知向量,且,则tanx=[ ]A.0B.1C.2D.”考查相似的试题有:
- 已知,则 .
- 已知a、b、c是△ABC中∠A、∠B、∠C的对边,a=43,b=6,cosA=-13.(1)求c;(2)求cos(2B-π4)的值.
- 已知sinθ=1-a1+a,cosθ=3a-11+a,若θ是第二象限角,求实数a的值.
- 满足sinsinx+coscosx=的锐角x= .
- 设定义在区间(0,)上的函数y=sin2x的图象与y=cosx图象的交点横坐标为α,则tanα的值为( )。
- 在锐角△ABC中,若tanA=t+1,tanB=t-1,则t的取值范围为______.
- 已知sin=,那么cosα=________.
- 已知△ABC中,a,b,c分别为角A、B、C所对的边;三内角A、B、C成等差数列.(1)求sinB的值;(2)若cosC=45,求sinA的值.
- .
- ( )A.B.C.D.