本试题 “在底面半径为r,高为h,全面积为πa2的圆锥中.(1)写出h关于r的函数;(2)当底面半径r为何值时,圆锥体积最大?最大体积是多少?” 主要考查您对函数的单调性、最值
柱体、椎体、台体的表面积与体积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性、最值
- 柱体、椎体、台体的表面积与体积
单调性的定义:
1、对于给定区间D上的函数f(x),若对于任意x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),则称f(x)是区间上的增函数;当x1<x2时,都有f(x1)>f(x2),则称f(x)是区间D上的减函数。
2、如果函数y=f(x)在区间上是增函数或减函数,就说函数y=f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。如果函数y=f(x)在区间D上是增函数或减函数,区间D称为函数f(x)的单调增或减区间
3、最值的定义:
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最大值.
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最小值
判断函数f(x)在区间D上的单调性的方法:
(1)定义法:其步骤是:
①任取x1,x2∈D,且x1<x2;
②作差f(x1)-f(x2)或作商 ,并变形;
,并变形;
③判定f(x1)-f(x2)的符号,或比较 与1的大小;
与1的大小;
④根据定义作出结论。
(2)复合法:利用基本函数的单调性的复合。
(3)图象法:即观察函数在区间D上部分的图象从左往右看是上升的还是下降的。
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
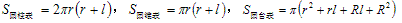
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,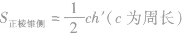 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,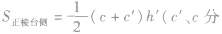  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
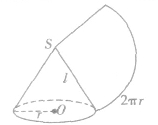 |
圆锥的侧面展开图是扇形: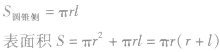 |
 |
| 圆台 |
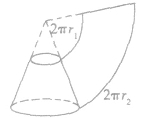 |
圆台的侧面展开图是扇环: |
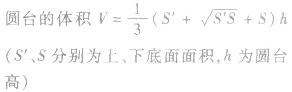 |
| 球 |
 |
 |
 |
与“在底面半径为r,高为h,全面积为πa2的圆锥中.(1)写出h关于...”考查相似的试题有:
- 判断函数y=的单调区间。
- 函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为[ ]A.(-1,1)B.(-1,+∞)C.(-∞,-1)...
- 设g(x)=x2+1,x≤0-2x,x>0,则使g(x)=5的x的值为______.
- 已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+≤2f(1),则a的取值范围是 ( )A.[1,2]...
- 设函数f(x)=lg(x2+ax-a),若f(x)的值域为R,则a的取值范围是______.
- 已知函数f(x)=x+2x,若f(a-2)=a,则a=______.
- 设偶函数对任意,都有,且当时,,则=" "A.10B.C.D.
- 将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了( )A.B.C.D.
- 已知各面均为等边三角形的四面体的棱长为2,则它的表面积是( )。
- (本小题满分8分)如图四边形为梯形,,,求图中阴影部分绕旋转一周所形成的几何体的表面积和体积。