1、全称量词与全称命题：
①全称量词：短语“对所有的”，“对任意的”在陈述中表示整体或全部的含义，逻辑中通常叫做全称量词，并用符号“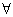”表示；
②全称命题：含有全称量词的命题，叫做全称命题
③全称命题的格式：“对M中任意一个x，有p（x）成立”的命题，记为?x∈M，p（x），读作“对任意x属于M，有p（x）成立”。
2、存在量词与特称命题：
①存在量词：短语“存在一个”，“至少有一个”在陈述中表示个别或者一部分的含义，在逻辑中通常叫做存在量词，并用符号“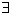”表示。
②特称命题：含有存在量词的命题，叫做特称命题；
③“存在M中的一个x₀，使p（x₀）成立”的命题，记为?x₀∈M，p（x₀），读作“存在一个x₀属于M，使p（x₀）成立”。
3、全称命题的否定：
一般地，对于含有一个量词的全称命题的否定，有下面的结论：
全称命题p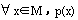：，它的否命题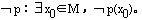
4、特称命题的否定：
一般地，对于含有一个量词的特称命题的否定，有下面的结论：
特称命题p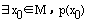：，其否定命题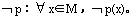

回归直线：

如果散点图中点的分布从整体上看大致在一条直线附近，我们就称这两个变量之间具有线性相关关系，这条直线叫做回归直线；

最小二乘法：

使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法。

回归直线方程：

，
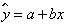其中。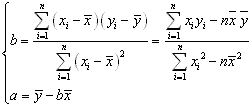

回归分析是处理变量相关关系的一种常用数学方法，其步骤为：

（1）确定特定量之间是否有相关关系，如果有，那么就找出他们之间贴近的数学表达式；
（2）根据一组观察值，预测变量的取值及判断变量取值的变化趋势；
（3）求出回归直线方程。

几何概型的概念：

如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）称比例，则称这样的概率模型为几何概率模型，简称为几何概型。

几何概型的概率：

一般地，在几何区域D中随机地取一点，记事件＂该点落在其内部一个区域d内＂为事件A，则事件A发生的概率。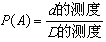
说明：（1）D的测度不为0；
（2）其中＂测度＂的意义依D确定，当D分别是线段，平面图形，立体图形时，相应的＂测度＂分别是长度，面积和体积；
（3）区域为＂开区域＂；
（4）区域D内随机取点是指：该点落在区域内任何一处都是等可能的，落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关．

几何概型的基本特点：

（1）试验中所有可能出现的结果（基本事件）有无限多个；
（2）每个基本事件出现的可能性相等．