本试题 “已知=2,=,∠AOB=150°,点C在∠AOB内,且∠AOC=30°,设(m,n∈R),则( ) A. B. C. D.” 主要考查您对相等向量与共线向量的定义
平面向量基本定理及坐标表示
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 相等向量与共线向量的定义
- 平面向量基本定理及坐标表示
相等向量的定义:
长度相等且方向相同的两个向量叫相等向量。
共线向量的定义:
方向相同或相反的非零向量,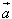 平行于
平行于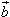 ,记作:
,记作: 。
。
规定零向量和任何向量平行。
注意:相等向量一定是共线向量,但共线向量不一定相等。表示共线向量的有向线段不一定在同一直线上,向量可以平移。
平行向量与相等向量的关系:
(l)平行向量只要求方向相同或相反即可,用有向线段表示平行向量时,向量所在的直线重合或平行.
(2)平行向量要求两个向量均为非零向量,规定:零向量与任一向量平行,记作 ;相等向量则没有这个限制,零向量与零向量相等.
;相等向量则没有这个限制,零向量与零向量相等.
(3)借助相等向量,可以把一组平行向量移动到同一直线上,因此,平行向量也叫做共线向量.(4)平行向量不一定是相等向量,但相等向量一定是平行向量.
向量共线的理解:
(1)两个非零向量平行的充要条件是这两个向量所在直线平行或重合.
(2)两个平行的非零向量在其方向与模两个要素上可能出现以下四种情况:
①方向相同,长度相同;
②方向相同,长度不同;
③方向相反,长度相同;
④方向相反,长度不同,
两个向量相等的理解:
(1)两个向量的长度相等,这两个向量不一定相等.
(2)两个向量相等,它们的起点和终点不一定相同.
(3)若a=b,b=c,则必有a=c.
平面向量的基本定理:
如果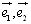 是同一平面内的两个不共线的向量,那么对这一平面内的任一向量
是同一平面内的两个不共线的向量,那么对这一平面内的任一向量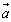 存在唯一的一对有序实数
存在唯一的一对有序实数 使
使 成立,不共线向量
成立,不共线向量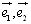 表示这一平面内所有向量的一组基底。
表示这一平面内所有向量的一组基底。
平面向量的坐标运算:
在平面内建立直角坐标系,以与x轴、y轴方向相同的两个单位向量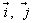 为基底,则平面内的任一向量
为基底,则平面内的任一向量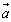 可表示为
可表示为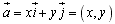 ,称(x,y)为向量
,称(x,y)为向量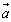 的坐标,
的坐标,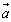 =(x,y)叫做向量
=(x,y)叫做向量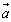 的坐标表示。
的坐标表示。
基底在向量中的应用:
(l)用基底表示出相关向量来解决向量问题是常用的方法之一.
(2)在平面中选择基底主要有以下几个特点:①不共线;②有公共起点;③其长度及两两夹角已知.(3)用基底表示向量,就是利用向量的加法和减法对有关向量进行分解。
用已知向量表示未知向量:
用已知向量表示未知向量,一定要结合图像,可从以下角度如手:
(1)要用基向量意识,把有关向量尽量统一到基向量上来;
(2)把要表示的向量标在封闭的图形中,表示为其它向量的和或差的形式,进而寻找这些向量与基向量的关系;
(3)用基向量表示一个向量时,如果此向量的起点是从基底的公共点出发的,一般考虑用加法,否则用减法,如果此向量与一个易求向量共线,可用数乘。
与“已知=2,=,∠AOB=150°,点C在∠AOB内,且∠AOC=30°,设(m,n∈...”考查相似的试题有:
- 已知a=(2,-1,3),b=(-4,2,x),且a∥b,则x=______.
- 已知点A(2,3),B(5,4),C(10,8),若AP=AB+λAC(λ∈R),求当点P在第二象限时,λ的取值范围.
- 若a=(1,2),b=(-1,1),ka+b与a-b共线,则k的值是( )A.2B.1C.0D.-1
- 若a=(6,-8),则与a平行的单位向量是______.
- 在中,,.若点满足,则( )A.B.C.D.
- 已知向量a=(2,x2,x),b=(x,1,2),其中x>0,若a∥b,则x=______.
- 已知、的夹角为则
- 已知a=(-2,2),b=(3,1),则与a+2b同向的单位向量为______.
- 四个分别满足下列条件,(1); (2);(3),; (4)则其中是锐角三角形有 ( )A.1个B.2个C.3个D.4个
- 已知向量a=(1,2),b=(-3,2).(1)求|a+b|和|a-b|;(2)当k为何值时,(ka+b)∥(a-3b).