本试题 “给出下列四个结论:①当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P,则过点P且焦点在y轴上的抛物线的标准方程是x2=y;②已知双曲线的右焦点为(5,0),一...” 主要考查您对双曲线的标准方程及图象
双曲线的性质(顶点、范围、对称性、离心率)
抛物线的标准方程及图象
抛物线的性质(顶点、范围、对称性、离心率)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 双曲线的标准方程及图象
- 双曲线的性质(顶点、范围、对称性、离心率)
- 抛物线的标准方程及图象
- 抛物线的性质(顶点、范围、对称性、离心率)
双曲线的标准方程:
(1)中心在原点,焦点在x轴上: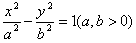 ;
;
(2)中心在原点,焦点在y轴上: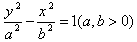 。
。
双曲线的图像:
(1)焦点在x轴上的双曲线的图像 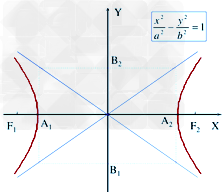 ;
;
(2)焦点在y轴上的双曲线的图像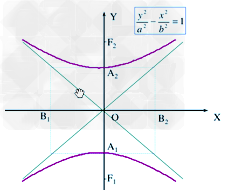 。
。
判断双曲线的焦点在哪个轴上:
判断双曲线的焦点在哪个轴上的方法看未知数前的系数,哪一个为正,焦点就在哪一个轴上.
定义法求双曲线的标准方程:
求动点的轨迹方程时,可利用定义先判断动点的轨迹,再写出方程.平面几何中的定理性质在解决解析几何问题时起着简化运算的作用,一定要注意应用,根据双曲线的定义,到两个定点的距离之差的绝对值是一个常数的点的轨迹是双曲线,可以求双曲线的标准方程,
待定系数法求双曲线的标准方程:
在求双曲线标准方程时,可先设出其标准方程,再根据双曲线的参数a,b,c,e的取值及相互之间的关系,求出a,b的值,已知双曲线的渐近线方程,求双曲线方程时,可利用共渐近线双曲线系方程 ,再由其他条件求λ.若焦点不确定时,要注意分类讨论.
,再由其他条件求λ.若焦点不确定时,要注意分类讨论.
利用双曲线的性质求解有关问题:
要解决双曲线中有关求离心率或求离心率范围的问题,应找好题中的等量关系或不等关系,构造出离心率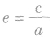 的关系式,这里应和椭圆中a,b,c的关系区分好,即
的关系式,这里应和椭圆中a,b,c的关系区分好,即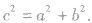
几种特殊的双曲线:
| 等轴双曲线 | 实轴和虚轴相等的双曲线叫做等轴双曲线.离心率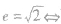 两条渐近线互相垂直 两条渐近线互相垂直 |
| 共轭双曲线 |
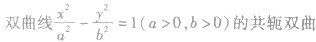
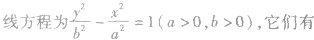

 |
| 共渐近线的双曲线 |

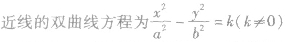 |
双曲线的离心率的定义:
(1)定义:双曲线的焦距与实轴长的比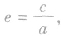 叫做双曲线的离心率.
叫做双曲线的离心率.
(2)e的范围:e>l.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.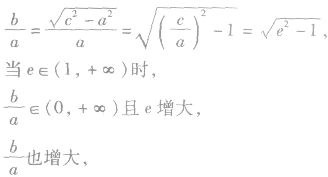
渐近线与实轴的夹角也增大。
双曲线的性质:
1、焦点在x轴上:顶点:(a,0),(-a,0);焦点:(c,0),(-c,0);
渐近线方程: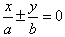 或
或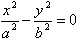 。
。
2、焦点在y轴上:顶点:(0,-a),(0,a);焦点:(0,c),(0,-c);
渐近线方程: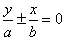 或
或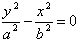 。
。
3、轴:x、y为对称轴,实轴长为2a,虚轴长为2b,焦距2c。
4、离心率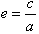 ;
;
5、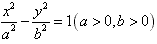 中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
双曲线的焦半径:
双曲线上的点 之间的线段长度称作焦半径,分别记作
之间的线段长度称作焦半径,分别记作

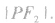
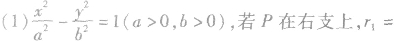
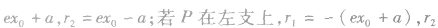
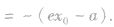
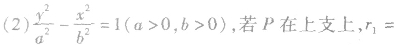
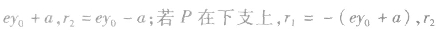

(2)焦点三角形:已知
 的两个焦点,P为双曲线上一点(异于顶点),
的两个焦点,P为双曲线上一点(异于顶点),
 的面积为
的面积为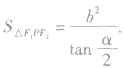
在解决与焦点三角形有关的问题时,应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用,还应注意灵活地运用平面几何、三角函数等知识来分析解决问题.
(3)基础三角形:如图所示,△AOB中,

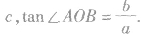
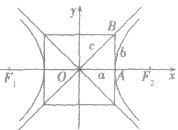
(5)自双曲线的焦点作渐近线的垂线,垂足必在相应的准线上,即过焦点所作的渐近线的垂线,渐近线及相应准线三线共点.
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切.
(7)双曲线
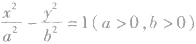 上一点P(x0,y0)处的切线方程是
上一点P(x0,y0)处的切线方程是
(8)双曲线划分平面区域:对于双曲线
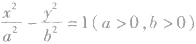 ,我们有:P(x0,y0)在双曲线内部(与焦点共区域)
,我们有:P(x0,y0)在双曲线内部(与焦点共区域)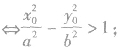 P(x0,y0)在双曲线外部(与焦点不其区域)
P(x0,y0)在双曲线外部(与焦点不其区域)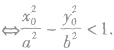
抛物线的标准方程及图像(见下表):

抛物线的标准方程的理解:
①抛物线的标准方程是指抛物线在标准状态下的方程,即顶点在原点,焦点在坐标轴上;
②抛物线的标准方程中的系数p叫做焦参数,它的几何意义是:焦点到准线的距离.焦点到顶点以及顶点到准线的距离均为
③抛物线的标准方程有四种类型,所以判断其类型是解题的关键,在方程的类型已确定的前提下,由于标准方程只有一个参数p,所以只需一个条件就可以确定一个抛物线的方程;
④对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,得出其异同点。
共同点:
a.原点在抛物线上;
b.焦点都在坐标轴上;
c.准线与焦点所在轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的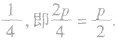
不同点:
a.焦点在x轴上时,方程的右侧为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;
b.开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
求抛物线的标准方程的常用方法:
(1)定义法求抛物线的标准方程:定义法求曲线方程是经常用的一种方法,关键是理解定义的实质及注意条件,将所给条件转化为定义的条件,当然还应注意特殊情况.
(2)待定系数法求抛物线的标准方程:求抛物线标准方程常用的方法是待定系数法,为避免开口不确定,分成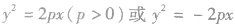 (p>0)两种情况求解的麻烦,可以设成
(p>0)两种情况求解的麻烦,可以设成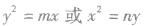 (m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
(m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
抛物线的性质(见下表):

抛物线的焦点弦的性质:
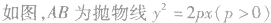
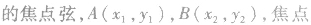

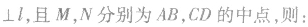

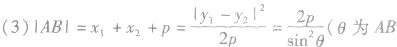

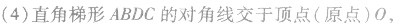


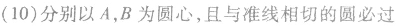
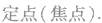
关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部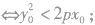 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部
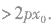
(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
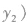 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F,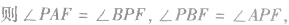 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。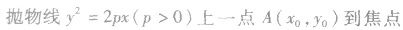
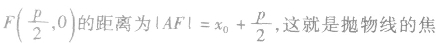
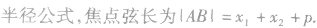
与“给出下列四个结论:①当a为任意实数时,直线(a-1)x-y+2a+1=0...”考查相似的试题有:
- 已知双曲线的渐近线为,焦点坐标为(﹣4,0),(4,0),则双曲线方程为[ ]A.B.C.D.
- 若方程x2m+y2m+3=1表示焦点在y轴上的双曲线,则m的取值范围为______.
- 若双曲线的渐近线方程为y=±32x,则其离心率为( )A.132B.133C.132或133D.213或
- 若双曲线的渐近线方程是,则该双曲线的离心率是[ ]A.B.C.D.
- 如果椭圆x29+y2k2=1与双曲线x2k-y23=1的焦点相同,则k的取值范围为( )A.2B.k>3C.k=2或k=4D.0<k<2
- 在平面直角坐标系xOy中,抛物线y2=4x的焦点为F,点P在抛物线上,若PF=2,则点P到抛物线顶点O的距离是______.
- 以抛物线x2=2y上点P(2,2)为切点的切线,与其准线交点的横坐标为( )A.-12B.-54C.34D.114
- 已知点A是双曲线的渐近线与抛物线y2=2px(p>0)的交点,F是抛物线的焦点,且AF⊥x轴,则双曲线的离心率为[ ]A、2B、C、D、
- 抛物线y2=10x的焦点到准线的距离是[ ]A.B.5C.D.10
- 过抛物线y2=4x的焦点作直线l,交抛物线于A,B两点,若线段AB中点的横坐标为3,则|AB|等于______.