本试题 “设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2005(x)=[ ]A.sinxB.-sinxC.cosxD.-cosx” 主要考查您对导数的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 导数的运算
常见函数的导数:
(1)C′=0 ;(2)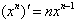 ;(3)
;(3)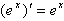 ;(4)
;(4) ;(5)
;(5)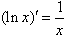 ;(6)
;(6)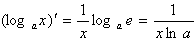 ;(7)
;(7)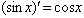 ;(8)
;(8)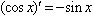
导数的四则运算:
(1)和差: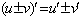
(2)积: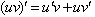
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: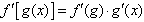
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
发现相似题
与“设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn...”考查相似的试题有:
- 在曲线y=x2+2的图象上取一点(1,3)及附近一点(1+△x,3+△y),则lim△x→0△y△x=______.
- 设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,g(-2)=0且 >0,则 不等式g (x)f(x) <0的解集是( )A.(-2, 0)∪(2,...
- 若函数,在处有极值,则等于( )A.2B.1C.D.0
- 已知函数f(x)=-x3+3f′(2)x,令n=f′(2),则二项式(x+2x)n展开式中常数项是第______ 项.
- 已知f(x)的导数是f′(x),且f(x)=x2+2x•f′(1),则f′(1)等于( )A.-2B.2C.1D.-4
- 已知a为实数,f(x)=(x2-4)(x-a).(1)求导数f′(x).(2)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值.(3...
- 已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(2013)-lnx,则f′(2013)=( )A.1B.-1C.12013D.无法确定
- 已知l是曲线的倾斜角最小的切线,则l的方程为____________.
- y=x3+ax+1的一条切线方程为y=2x+1,则a=______.
- 函数y=cos(2x2+x)的导数是______.