本试题 “(本小题满分16分)已知数列满足.(1)求数列的通项公式;(2)对任意给定的,是否存在()使成等差数列?若存在,用分别表示和(只要写出一组);若不存在,...” 主要考查您对正弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即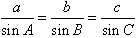 =2R。
=2R。
有以下一些变式:
(1)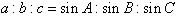 ;
;
(2)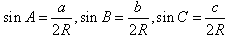 ;
;
(3)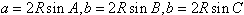 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 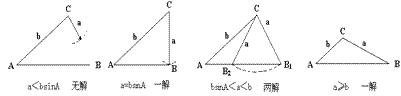
也可根据a,b的关系及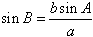 与1的大小关系来确定。
与1的大小关系来确定。
发现相似题
与“(本小题满分16分)已知数列满足.(1)求数列的通项公式;(2...”考查相似的试题有:
- 在△ABC中,BC=,AC=3,sinC=2sinA,(1)求AB的值;(2)求sin的值。
- 在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足sinA+cosA=2,(Ⅰ)求A的大小;(Ⅱ)现给出三个条件:①a=2;②B=45°;③c=b,...
- 已知△ABC的面积S=53,AB=4,最大边AC=5,那么BC边的长为( )A.3B.3C.4D.21
- 在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足(2b-3c)cosA=3acosC.(1)求A的大小;(2)现给出三个条件:①a=2;②B=4...
- 求证:在△ABC中,其中α,β,γ是三角形的内角,cosα=sin2β+sin2γ-sin2α2sinβ•sinγ.
- 已知中,,,,那么
- (本题满分12分)在△ABC中,角A、B、C所对的边分别为a、b、c(其中),设向量,,且向量为单位向量.(模为1的向量称作单位向...
- 某体育学校决定修建一条三角形多功能比赛通道(如图),AB段是跑道,BC段是自行车道,CA段是游泳道,试根据图中数据计算自行...
- (1)在中,已知,,,求及、的值;(2)在△ABC中,若则△ABC的形状是什么?
- 在△ABC中,a,b,c分别为角A,B,C的对边,若且,则sinB=[ ]A.B.C.D.